Вынужденные колебания в системе с двумя степенями свободы
|
|
(7.11) |
Видно, что связь между координатами линейная. Естественно, что уравнения колебаний для нормальных координат будут такими
|
|
(7.12) |
Особенностью уравнений движения, записанных в нормальных координатах, является отсутствие членов, описывающих связи между системами, т. е. система разбивается на две независимые системы. За связь, вообще говоря, отвечает слагаемое, содержащее произведение парциальных координат в уравнении Лагранжа. Следовательно, в выражениях для кинетической и потенциальной энергий системы, записанных в нормальных координатах, не содержится произведения координат.
|
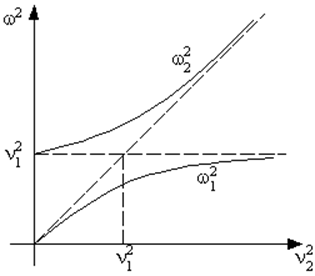
Рис. 60. График Вина. |
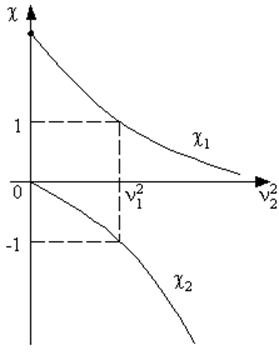
Рис. 61. Зависимость коэффициентов распределения от парциальных частот. |
Рассмотрим зависимость нормальных частот системы от соотношения парциальных частот маятников. С помощью соотношения (7.7) можно построить график зависимости квадратов нормальных частот от парциальных. Для определённости будем считать, что изменяется только одна из парциальных частот, например n2. Тогда график такой зависимости, называемый графиком Вина, будет иметь вид, представленный на рис. 60. Как видно, при любом n2 парциальные частоты лежат между собственными частотами. Это свойство является общим для любых консервативных систем с двумя степенями свободы.
Из уравнения (7.7) видно, что если парциальные частоты сильно различаются, то при не слишком сильной связи (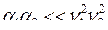 ), нормальные частоты близки к парциальным частотам (w1,2 » n1,2). По мере сближения парциальных частот нормальные частоты отходят от парциальных. Наибольшее отличие w1,2 от n1,2 наблюдается вблизи равенства парциальных частот (n1 = n2).
), нормальные частоты близки к парциальным частотам (w1,2 » n1,2). По мере сближения парциальных частот нормальные частоты отходят от парциальных. Наибольшее отличие w1,2 от n1,2 наблюдается вблизи равенства парциальных частот (n1 = n2).
Построим теперь график, показывающий поведение коэффициентов c1 и c2 при изменении парциальной частоты n2 (рис. 61). Так как n1 всегда больше w1 и меньше w2, то из соотношений (7.8) следует, что c1 всегда больше нуля (c1 > 0), а c2 всегда меньше нуля (c2 < 0). Поэтому колебания на частоте w1 всегда происходят в фазе (синфазны), а колебания на частоте w2 всегда противофазны.
В общем случае величину физической связи (обмен энергией) между парциальными системами характеризуют связностью
|
|
(7.13) |
которая определяется не только коэффициентами связи, но и близостью значений парциальных частот. Если связность мала (s << 1), когда обмен энергией между парциальными системами мал, собственные частоты близки к соответствующим парциальным частотам (w1,2 » n1,2). Также, при малой связности обмен энергией между парциальными системами незначителен.
7.2. Вынужденные колебания в системе с двумя степенями свободы
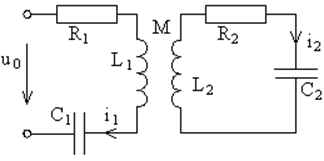
Рассмотрим вынужденные колебания в системе из двух индуктивно связанных контуров, в один из которых включен источник внешнего переменного напряжения u0(t) = U0cos(w0t) (рис. 62).
|
Запишем уравнения колебаний для этих контуров, пренебрегая вначале затуханием (R1 = R2 = 0):
Уравнения колебаний токов принимают в этом случае вид |
Рис. 62. Схема связанных контуров при внешнем воздействии. |
|
|
(7.14) |
где обозначено
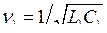 ,
, 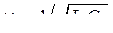 ,
, 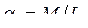 ,
, 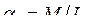 .
.
Система линейная, следовательно, в силу принципа суперпозиции, колебания в системе будут состоять из собственных колебаний с частотами w1 и w2 и вынужденных колебаний с частотой внешней силы w0. Собственные колебания ищем в виде
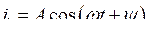 ,
, 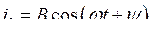 .
.
Подставив в (7.14), получим следующую систему уравнений относительно амплитуд A и B:
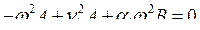 ,
, 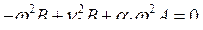 .
.
Известно, что система имеет нетривиальное решение, если её детерминант равен нулю:
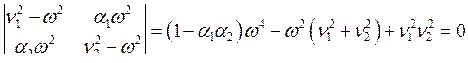 .
.
Решив это уравнение, можно найти выражение для собственных частот:
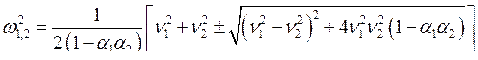 .
.
Нетрудно найти выражение для коэффициентов распределения амплитуд:
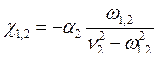 .
.
Вынужденные колебания происходят на частоте внешней силы. Так как нет диссипации, то сдвиг фаз будет равен нулю, следовательно, решение уравнений (7.14) для вынужденных колебаний будем искать в виде
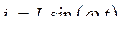 ,
, 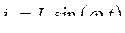 .
.
Подставляя в исходное уравнение (7.14), получим
|
|
(7.15) |
Из второго уравнения найдём коэффициент распределения амплитуд вынужденных колебаний
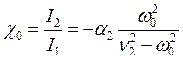 .
.
Видно, что c0(w0 = w1) = c1, а c0(w0 = w2) = c2. Таким образом, отношение амплитуд вынужденных колебаний в контурах совпадает с отношением амплитуд при собственных колебаниях (на соответствующей частоте). Решая систему (7.15), получим выражения для амплитуд:
|
|
(7.16) |
|
Рис. 63. Зависимости I1 и I2 для консервативной системы с двумя степенями свободы от частоты внешней силы. |
На рис. 63 приведены зависимости I1 и I2 от частоты внешней силы w0. В точках w0 = w1 и w0 = w2 амплитуды I1 и I2 обращаются в бесконечность. Таким образом, в системе с двумя степенями свободы резонансное увеличение амплитуды колебаний происходит на обеих собственных частотах системы. При w0 < n2 токи совершают противофазные колебания, а при w0 > n2 — синфазные. В точке w0 = n2 амплитуда I1 обращается в нуль, т. е. происходит гашение колебаний в первом контуре. Это явление легко объяснить тем, что в отсутствие потерь на частоте n2 обратная реакция второго контура на первый точно равна внешнему воздействию. Во втором контуре колебания не обращаются в нуль ни при каком конечном w0. Частота успокоения в общем случае зависит от того, в какую из ветвей сложного контура включена внешняя ЭДС. Она всегда равна парциальной частоте того контура, |
который получается при разрыве цепи в точке включения ЭДС.
Выясним физическую причину отсутствия колебания в первом контуре при w0 = n2. Для этого рассчитаем ЭДС, наводимую в первом контуре на этой частоте колебаниями второго контура (воспользуемся уравнением (7.16), положив w0 = n2):
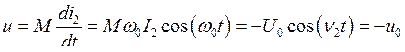 .
.
Как видно, u в точности компенсирует внешнюю ЭДС, поэтому вынужденные колебания в первом контуре на частоте n2 не происходят.
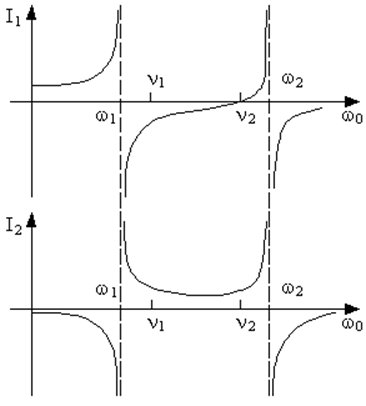
Задачу о вынужденных колебаниях в диссипативной системе удобно решать с помощью МКА. Рассматривая систему связанных контуров (рис. 62) относительно входных зажимов как линейный двухполюсник с полным сопротивлением Z, получим из уравнений (7.14)
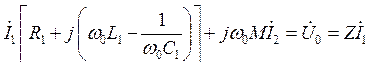 ,
, 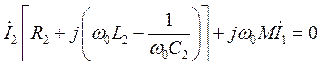 .
.
Решая эту систему уравнений, находим полное сопротивление
|
|
(7.17) |
Условие резонанса в этом контуре сводится к равенству нулю реактивного сопротивления, т. е. ImZ(w0) = 0. Введём относительные расстройки контуров
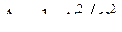 ,
, 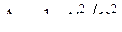
и парциальные декременты затухания
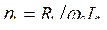 ,
, 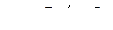 .
.
Тогда условие резонанса будет иметь вид:
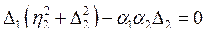 .
.
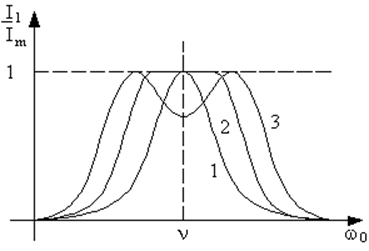
В случае одинаковых парциальных частот контуров (n1 = n2 = n) относительные расстройки равны (D1 = D2 = D), и мы получаем очень простое условие резонанса:
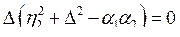 .
.
Из этого уравнения находим три значения D:
 ,
, 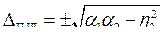 .
.
Следовательно, система двух связанных контуров имеет три резонансные частоты
 ,
, 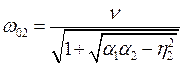 ,
, 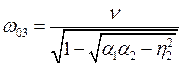 .
.
|
Рис. 64. Резонансные кривые двух связанных контуров с равными парциальными частотами при коэффициенте связи меньшем критического (1), равным критическому (2) и большем критического (3). |
Если затухание во втором контуре велико ( |
Рассмотрим теперь особенности вынужденных колебаний в двухконтурной системе без потерь при одновременном действии внешних источников в обоих контурах (u01 и u02). Уравнения колебаний для токов в таких контурах имеют вид:
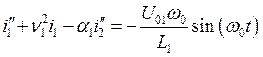 ,
, 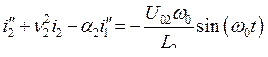 .
.
Мы считаем, что внешние источники действуют на одной и той же частоте и синфазны, т. е. u01 = U01cos(w0t), u02 = U02cos(w0t). Решая методом комплексных амплитуд, находим
|
|
(7.18) |
Из (7.18) вытекают два интересных следствия. Это, во-первых, принцип взаимности, который гласит: амплитуда вынужденных колебаний во втором контуре при включении некоторого источника в первый равна амплитуде колебаний в первом контуре, если тот же источник включить во второй контур, т. е. I2(U02 = 0, U01 = U) = I1(U01 = 0, U02 = U). Принцип взаимности является следствием линейности системы. Этот принцип можно доказать, хотя и более громоздко, и для контуров с потерями. Важное для радиофизики следствие принципа взаимности — диаграммы направленности антенн на излучение и на приём одинаковы.
Вторая особенность вынужденных колебаний в системе с двумя степенями свободы заключается в том, что при определённом соотношении между амплитудами внешних источников в системе может отсутствовать резонанс, даже если частота внешнего источника совпадает с одной из нормальных (собственных) частот. Это происходит, когда и числитель и знаменатель в соотношениях (7.18) обращаются в нуль. Например, для частоты w0 = w1 соотношение между амплитудами имеет вид
|
|
(7.19) |
Условие (7.19) называется условием ортогональности внешней силы собственному колебанию с частотой w1.
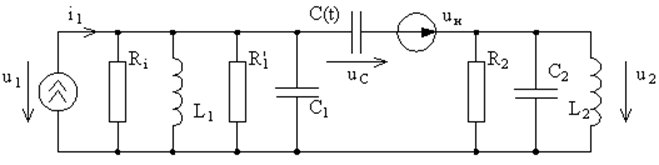
7.3. Двухконтурный параметрический усилитель
|
Рис. 65. Схема двухконтурного параметрического усилителя с генератором накачки и нелинейной ёмкостью. |
Рассмотрим конденсатор с переменной ёмкостью
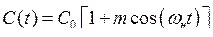 ,
,
меняющейся под действием напряжения накачки uн(t) = Uнcos(wнt). Пусть к этому конденсатору приложено переменное напряжение uС(t) = U1cos(w1t + j), тогда емкостной ток составит
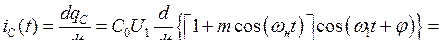
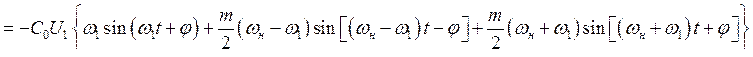 .
.
Таким образом, в спектре тока имеются компоненты с частотами w1, wн + w1 и wн — w1. Эти частоты можно выделить с помощью достаточно высокодобротных контуров, настроенных на частоты w1 и w2 = wн ± w1 и связанных общей нелинейной ёмкостью (рис. 65).
Полное сопротивление потерь в первом контуре будет R1 = R‘1||Ri (где Ri — внутреннее сопротивление источника сигнала). Пусть этот контур настроен на частоту близкую к частоте усиливаемого сигнала, т. е. n1 » w1. Соответственно, второй контур L2C2R2 настроен на частоту w2 = wн ± w1 (n2 » w2). Рассмотрим случай, когда парциальные частоты n1 и n2 контуров далеки друг от друга так, что связанность мала. В этом случае нормальные частоты близки к парциальным (сдвиг между парциальной и соответствующей нормальной частотами небольшой и мы можем считать, что он лежит в полосе пропускания контуров, т. е. каждый контур резонирует на своей собственной частоте). Таким образом, свою частоту контур резко усилит, остальные ослабит.
При достаточно высокой добротности контуров сопротивления каждого контура для частот, далёких от его парциальной частоты, практически равны нулю. Таким образом, контур является активной нагрузкой лишь в небольшой области частот вблизи своей парциальной частоты. В рассматриваемой нами схеме в основном контуре активная мощность может выделяться только на частоте w1, а в дополнительном — на одной из частот w2 = wн ± w1. Таким образом, раз мы в каждом контуре можем следить только за одной частотой, то для этих частот запишем уравнения гармонического баланса
|
|
(7.20) |
Пусть в качестве нелинейной ёмкости взят варикап. Тогда, как известно,
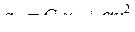 .
.
Поскольку uC = u1 + uн — u2, тогда в рамках гармонического баланса мы должны положить uн = Aнcos(wнt), u1 = A1cos(w1t + y1), u2 = A2cos(w2t + y2) (фазы y1 и y2 отсчитаны от напряжения накачки). Подставляя эти выражения в выражение для заряда, получим соотношения для составляющих заряда на ёмкости C на частотах w1 и w2:
![]() ,
,
![]() .
.
Здесь (как и далее) верхний знак соответствует случаю w2 = wн + w1, а нижний — w2 = wн — w1.
В этом случае уравнение гармонического баланса (7.20) при воздействии гармонического сигнала i1 = I1cos(w1t + j) принимает вид:
|
|
(7.21) |
|
|
(7.22) |
Немного упростим эти выражения, введя парциальные частоты n1 и n2, расстройки x1 и x2, добротности Q1 и Q2 контуров усилителя:
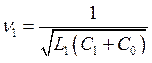 ,
, 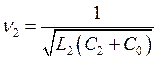 ;
; 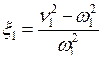 ,
, 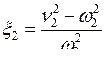 ;
;
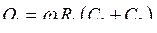 ,
, 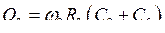 .
.
Тогда в этих обозначениях уравнение (7.21) примет вид
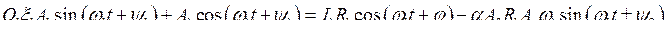 .
.
Полученное соотношение должно выполняться в любой момент времени, поэтому в нём следует приравнять в правой и левой частях коэффициенты при cos(w1t + y1) и sin(w1t + y1). Положим в правой части j = y1 + (j — y1); ±y2 = y1 + (±y2 — y1), тогда после простых тригонометрических преобразований правой части, получим
|
|
(7.23) |
|
|
(7.24) |
Аналогично из (7.22) получаем условие баланса
|
|
(7.25) |
|
|
(7.26) |
Возведём в квадрат (7.25) и (7.26) и сложим, тогда можно получить
|
|
(7.27) |
Выразим cos(±y2 — y1) и sin(±y2 — y1) из (7.25) и (7.26) и подставим в (7.23) и (7.24):
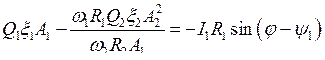 ,
,
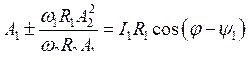 .
.
Возведём левые и правые части этих соотношений в квадрат и сложим, а затем вместо A2 подставим его выражение из (7.27). В результате чего получается выражение для амплитуды колебаний в первом контуре в зависимости от параметров усилителя:
|
|
(7.28) |
Напомним, что верхний знак соответствует случаю w2 = wн + w1, а нижний — w2 = wн — w1. Полученное выражение показывает, что амплитуда параметрического усилителя с низкочастотной накачкой (wн = w2 — w1) существенно отличается от амплитуды усилителя с высокочастотной накачкой (wн = w2 + w1). Рассмотрим теперь отдельно каждый из этих случаев.
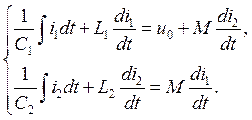
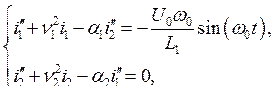
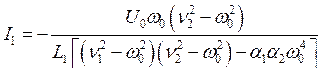 ,
, 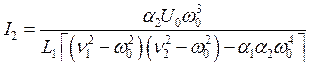 .
.
 .
.
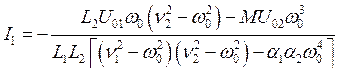 ,
,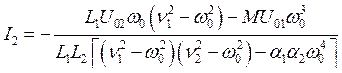 .
.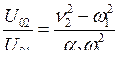 .
.
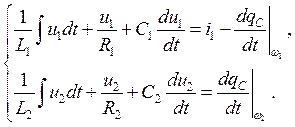
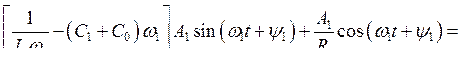
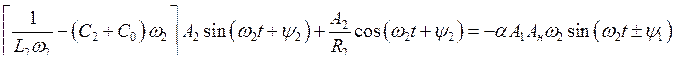 .
.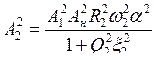 .
.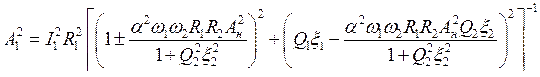 .
.

