Закон ома

·  В  различных веществах содержится  различное количество электронов, а атомы, между которыми эти электро­ны движутся, имеют различное расположение. Поэтому сопротив­ление проводников электрическому току зависит от материала, из которого они изготовлены, от длины и площади поперечного сече­ния проводника. Если сравнить два проводника, изготовленных из одного и того же материала, то более длинный проводник имеет большее сопротивление при равных площадях поперечных сечений, а проводник с большим поперечным сечением имеет меньшее сопро-тивление при равных длинах.

·  Для оценки электрических свойств материала проводника слу­жит удельное сопротивление — это сопротивление проводника дли­ной в 1 м и площадью поперечного сечения в 1 мм2. Удельное сопротивление обозначается буквой .

·  Если проводник, изготовленный из материала с удельным сопро­тивлением , имеет длину l метров и площадь поперечного сечения q квадратных  миллиметров,  то  сопротивление  всего  проводника

· 

·  Эта формула указывает на то, что сопротивление проводника прямо пропорционально удельному сопротивлению материала, из которого он изготовлен, а также его длине и обратно пропорцио­нально площади поперечного сечения.

·  Сопротивление проводников зависит от температуры, причем сопротивление металлических проводников с повышением темпе­ратуры увеличивается. Для каждого металла существует опреде­ленный, так называемый температурный,  коэффициент  сопротивления, который выражает прирост сопротивления проводника при измнении температуры на  10 С  отнесенный  к  1  ом  начального сопротивления.

·  Таким образом,  температурный  коэффициент  сопротивления

·   

·  где r1 — сопротивление проводника при температуре T1,

·    r2 — сопротивление того же проводника при температуре T2,

·  Поясним выражение для температурного коэффициента сопро­тивления на примере. Положим, что медный линейный провод при температуре T1= 15° С имеет сопротивление r1 = 75 ом, а при темпе­ратуре T2= 75°С  r2=93 ом. Следовательно, прирост сопротивления при изменении температуры на 75—15 = 60° С составляет 93—75 = = 18 ом. Таким образом, прирост сопротивления, соответствующий изменению температуры на 1°С, равен =0,3.

·  Для определения температурного коэффициента сопротивлений нужно этот прирост сопротивления  отнести  к  1  ом  начального сопротивления, т. е. разделить на 75:

· 

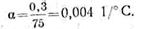
·  Соотношение между сопротивлениями r1 и r2:

· 

·  Следует иметь в виду, что это соотношение справедливо при не очень высоких температурах, а для измерения сопротивлений при температурах выше 100—150° С оно не может быть исполь­зовано.

·  Регулируемые сопротивления называются реостатами. Реоста­ты изготовляют из проволоки с большим удельным сопротивлением, например из нихрома. Сопротивление реостатов может изменяться равномерно или ступенями. Применяют также жидкостные реоста­ты, представляющие собой металлический сосуд, наполненный ка­ким-либо раствором, проводящим электрический ток, например рас­твором соды в воде. На схемах реостаты условно обозначают так, как показано на рис. 14, б.

·  Способность проводника пропускать электрический ток харак­теризуется проводимостью, которая представляет собой величину, обратную сопротивлению, и обозначается буквой g. Единицей изме­рения проводимости является   (сименс).

· 

·  Величина  обратная  удельному  сопротивлению  материала проводника, называется удельной проводимостью и обозначается буквой .

·  Таким образом, между удельным сопротивлением и  удельной  проводи­мостью вещества имеют место следующие соотношения:

· 

·  Пример 1. Определить длину медной проволоки диаметром  1 мм, имеющей сопротивление 15 ом, зная, что удельное сопротивление меди 0,0175  .

·  Решение: поперечное сечение провода равно:

· 

·  откуда

· 

· 

·  Пример 2. Определить  поперечное сечение нихромовой проволоки   = 1  , имеющей при длине 40 м сопротивление 50 ом.

·  Решение: 

· 

·  откуда

· 

·  Пример 3. Обмотка трансформатора, изготовленная из медного провода, в нерабочем состоянии при 15° С имела сопротивление r1=2 ом. При работе сопро­тивление ее стало равным r2=2,48 ом. Определить температуру обмотки в рабо­чем состоянии, зная, что температурный коэффициент меди 0,004.

·  Решение.

· 

·  откуда

·   

·  § 16. ЗАКОН ОМА

·  Соотношение между э. д. с, сопротивлением и силой тока в замкнутой цепи выражается законом Ома, который может быть сформулирован так: сила тока в замкнутой цепи прямо пропорцио­нальна электродвижущей силе и обратно пропорциональна сопро­тивлению всей цепи.

·  Ток в цепи протекает под действием э. д. с; чем больше э. д. с. источника энергии, тем больше и сила тока в замкнутой цепи. Сопротивление цепи препятствует прохождению тока, следователь­но, чем больше сопротивление цепи, тем меньше сила тока.

·  Закон Ома можно выразить следующей формулой:

· 

·  или

· 

·  где r — сопротивление внешней части цепи,

·  r0 — сопротивление внутренней части цепи.