ВУЗы по физике
Готовые работы по физике
Как писать работы по физике
Примеры решения задач по физике
Решить задачу по физике онлайнЗакон сохранения энергии и импульса
Задача 4. Ка-ноль мезон (K0) имеет массу покоя, равную 498 МэВ и среднее время жизни 6×10-8 с. На какое расстояние успеет переместиться эта частица до распада при энергии 2000 МэВ?
Решение. Среднее время жизни t ка-ноль мезона в лабораторной системе отсчета равно
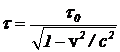. (10)
Из выражения полной энергии следует, что фактор Лоренца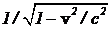 
равен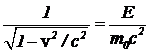 
, (11)
поэтому
t= t0. (12)
За это время частица переместится на расстояние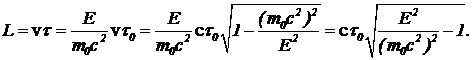 
(13)
Подставим численные данные, тогда
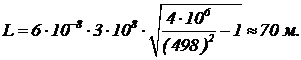
Задача 5. Выразите инвариантную массу m0 заряженной частицы с зарядом q, среднее время жизни t0, через энергию частицы E, радиус кривизны траектории R в магнитном поле индукции B и длину следа L, соединяющего точки рождения и распада в трековой камере.
2.4 Закон сохранения энергии и импульса
Задача 6. Найдите, чему равно наибольшее число пионов, которое может образоваться в результате столкновения протона с энергией Wp=5 ГэВ с покоящимся протоном. Энергия покоя пиона 140 МэВ. Энергия покоя протона 938 МэВ.
Решение. Пусть N – неизвестное пока число рожденных пионов. Минимально возможное значение инвариантной массы системы из двух протонов и N пионов равно (2mp+Nmp)c2, поэтому
(E+mpc2)2-(pc)2=[(2mp+Nmp)c2]2®N=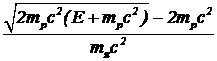
. (14)
Естественно, что ответ дает целая часть выражения (14). Подставляем:
N= »10.
Задача 7. Для получения нейтрино (n) высокой энергии используют явление распада заряженных пионов на лету по схеме p®mn. Получают пучок пионов высокой энергии Wp=10 ГэВ, которые на пути своего движения распадаются. Чему равна энергия нейтрино в лабораторный системе отсчета при движении распадного мюона (m) в системе центра масс под прямым углом к направлению движения пиона? Энергия покоя пиона 140 МэВ. Энергия покоя мюона 106 МэВ.
Решение. Нейтрино является безмассовой частицей, поэтому его энергия выражается через импульс формулой En=pnc. Таким образом, задача сводится к отысканию импульса нейтрино. Определим его вначале в системе центра масс. Полная энергия в системе центра масс равна энергии покоя пиона. После распада энергия распределяется между нейтрино и мюоном. Энергия нейтрино —
E0n=p0nc. (15)
Энергия мюона —
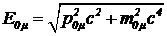, (16)
причем
p0m=p0n=p0. (17)
Из закона сохранения энергии
mpc2=p0c+ ®(mpc2— p0c)2=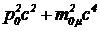
. (18)
Решение уравнения (18) относительно импульса нейтрино дает
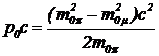. (19)
Уравнение (19) дает составляющую, перпендикулярную к направлению движения. Продольная составляющая в соответствии с условием задачи равна нулю.
Учтем, что до распада двигался только один пион. Распад не изменяет состояние движения центра масс, значит, скорость центра масс равна скорости пиона. Согласно (10),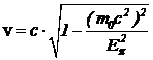 
. Подставим это в формулу преобразования Лоренца. С учетом (17) продольная составляющая импульса нейтрино
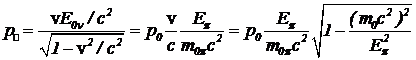. (20)
Полный импульс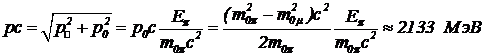 
. (21)
занятие 1.6.6
контрольная работа по теории относительности
вариант i
Задача 1. Полная энергия протона равна E=100mpc2.
а) Найдите отношение релятивистской массы протона к массе покоя.
б) Чему равна скорость протона?
в) Найдите отношение релятивистского импульса к классическому.
г) Чему равен радиус кривизны траектории протона в магнитном поле индукции 1 Тл? mpc2=938 МэВ.
Задача 2. Масса покоя мюона mm с2=106 МэВ, собственное время жизни tm=2.2 10-6с. Пусть родившиеся мюоны имеют кинетическую энергию 10600 МэВ. На каком расстоянии от места рождения число мюонов уменьшится в e раз?
Задача 3. Первоначально покоящийся протон при поглощении нейтрино (инвариантная масса равна нулю) может превратиться в нейтрон и позитрон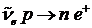 
. При какой минимальной энергии нейтрино возможно данное взаимодействие? mpc2=938 МэВ; mnc2=940 МэВ; mec2=0,51 МэВ.
Задача 4 [дополнительная]. Для получения нейтрино nm высокой энергии используют явление распада заряженных пионов на лету по схеме p®mn. Получают пучок пионов высокой энергии Wp =10 ГэВ, которые на пути своего движения распадаются. Чему равна максимальная энергия нейтрино, получаемых в этом процессе? Энергия покоя пиона 140 МэВ.
вариант ii
Задача 1. Кинетическая энергия частицы в 4 раза меньше энергии покоя.
а) Найдите отношение релятивистской массы частицы к массе покоя.
б) Чему равна скорость частицы?
в) Найдите отношение релятивистского импульса к классическому.
г) Чему равен радиус кривизны траектории частицы в магнитном поле индукции 0,01 Тл? mec2=0,51 МэВ?
Задача 2. Найдите собственное время жизни нейтрона по следующим данным: расстояние от Земли до Солнца, равное 1.5 1011 м, преодолевает только часть нейтронов, составляющая 1/e от рождающихся в момент вылета; полная энергия нейтронов 1050 МэВ; энергия покоя нейтрона 940 МэВ.
Задача 3. При какой минимальной энергии отрицательного каона K—, налетающего в пузырьковой камере на покоящийся протон, возможно взаимодействие K-p®W–K+K0? mKc2=494 МэВ; mpc2=938 МэВ; mWc2=1672 МэВ; mK0c2» mKc2.
Задача 4 [дополнительная]. Для получения нейтрино nm высокой энергии используют явление распада заряженных пионов на лету по схеме p®mnm. Получают пучок пионов высокой энергии Wp =10 ГэВ, которые на пути своего движения распадаются. Чему равна максимальная энергия нейтрино, получаемых в этом процессе? Энергия покоя пиона 140 МэВ. Энергия покоя мюона 106 МэВ?
МГМИМО
Скидка 30% по промокоду Diplom2020
Получи промокод на скидку 20%
Заказ дипломных работ