Трудности классической теории электропроводности
![]() .
.
Второе предположение теории позволяет оценить среднее расстояние между последовательными столкновениями электрона в металле ![]() (длину пробега). Выходит, что длина пробега равна межатомному расстоянию ионов решётки:
(длину пробега). Выходит, что длина пробега равна межатомному расстоянию ионов решётки:
![]() .
.
Из школьной физики известно, что межатомное расстояние — величина порядка одного ангстрема: Å=10-10 м. Отсюда, кстати, и оценка концентрации ионов в кристалле химически чистого металла, которая равна а—3.
Обратимся к предположению III. Дрейфовая — это та скорость, которая возникает под воздействием напряжённости поля движущих сил Е. Во всех практических случаях характерный размер неоднородностей такого поля значительно превосходит межатомное расстояние ионной матрицы. Значит, на длине свободного пробега электрона поле движущих сил можно считать однородным, а движение электрона равнопеременным с ускорением 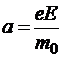 . Если, согласно предположению, при ударе электрона о решётку его скорость упорядоченного движения полностью теряется, то к концу свободного пробега электрон приобретает её максимальное значение
. Если, согласно предположению, при ударе электрона о решётку его скорость упорядоченного движения полностью теряется, то к концу свободного пробега электрон приобретает её максимальное значение
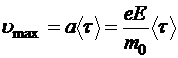 ,
,
где ![]() — время свободного пробега. Ясно, что
— время свободного пробега. Ясно, что
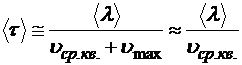 .
.
Дрейфовую скорость, очевидно, можно трактовать как среднюю скорость упорядоченного движения на длине свободного пробега. В соответствие с кинематикой равнопеременного движения:
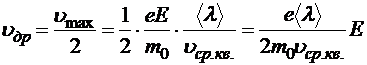
Тогда плотность тока
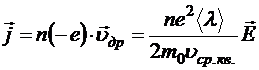
с учётом того, что дрейфовая скорость отрицательного носителя направлена против векторов ![]() и
и ![]() То есть получился закон Ома в дифференциальной форме
То есть получился закон Ома в дифференциальной форме 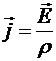 , где удельное сопротивление
, где удельное сопротивление
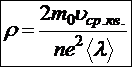 .
.
Итак, теория Д-Л позволяет получить дифференциальную форму закона Ома. Кроме этого, исходя из представлений этой теории, можно объяснить выражение объёмной плотности тепловой мощности: 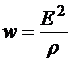 само по себе, не прибегая к равенству объёмных плотностей тепловой мощности и мощности движущих сил. Покажем это.
само по себе, не прибегая к равенству объёмных плотностей тепловой мощности и мощности движущих сил. Покажем это.
Пусть ![]() — энергия, сообщённая электрону на длине свободного пробега полем движущих сил. По предположению III она переходит в тепло.
— энергия, сообщённая электрону на длине свободного пробега полем движущих сил. По предположению III она переходит в тепло.
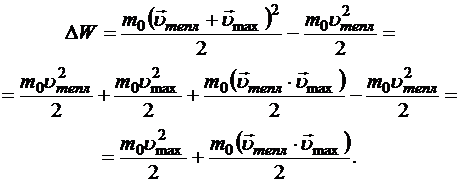
Усредняя по всем соударениям и учитывая, что из-за хаотичности теплового движения 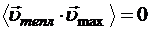 получим:
получим:
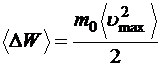 .
.
Пренебрегая разницей между ![]() и
и 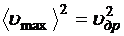 , имеем:
, имеем:
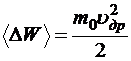 ,
,
То есть мы можем сказать, что в среднем в результате соударения электрон теряет только энергию упорядоченного движения. Используем полученное ранее выражение дрейфовой скорости:
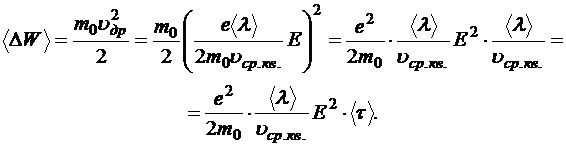
В единице объёма кристалла n электронов, каждый из которых испытывает 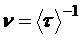 соударений в секунду. Следовательно, количество тепла, выделяющееся в единице объёма за единицу времени:
соударений в секунду. Следовательно, количество тепла, выделяющееся в единице объёма за единицу времени:
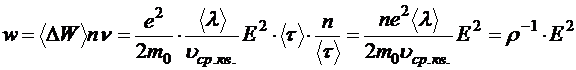 .
.
§18.3. Закон Видемана-Франца
Если в какой-либо среде возникает неравномерное распределение температуры T (неоднородное температурное поле), то оно порождает векторное поле плотности потока тепла
![]() ,
,
где k — коэффициент теплопроводности. Это соотношение называется законом Фурье. Из теории явлений переноса в идеальных газах, которая будет рассматриваться в следующем томе, известно, что
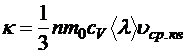 .
.
Здесь сV — удельная теплоёмкость идеального газа при постоянном объёме:
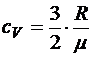 ,
,
R — универсальная газовая постоянная; m — молярная масса газа. Она равна произведению числа Авогадро на массу частицы газа:
![]() .
.
Тогда
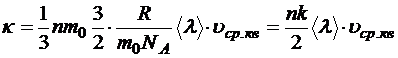 ,
,
поскольку, 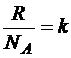 — постоянная Больцмана.
— постоянная Больцмана.
В металлах Видеман и Франц экспериментально установили закон, согласно которому
произведение коэффициента теплопроводности на удельное сопротивление одинаково для всех металлов при данной температуре.
Если считать, что в основном теплопроводность металлов определяется электронами проводимости (на это указывает то, что теплопроводность диэлектриков значительно хуже, чем металлов), то в соответствие с теорией Д-Л:
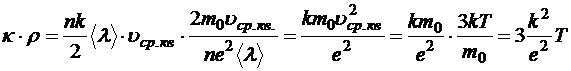 .
.
Мы видим, что, действительно, в выражение входят только мировые константы и температура. Кроме того, полученное теоретическое значение с точностью до 10% совпадает с измеренным в эксперименте. Таким образом, классическая теория электропроводности описывает закон Видемана-Франца, и это — самое большое её достижение.
§18.4. Трудности классической теории электропроводности
18.4.1. Удельное сопротивление
Из выражения удельного сопротивления теории Д-Л следует, что r данного металла прямо пропорциональна квадратному корню из абсолютной температуры:
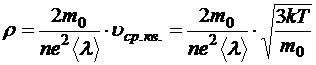 .
.
Но эксперимент опровергает корневую температурную зависимость. Оказывается, что
во всех металлах удельное сопротивление прямо пропорционально T.
18.4.2. Длина свободного пробега
Выразим длину свободного пробега через удельное сопротивление:
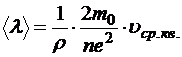 .
.
Даже при среднеквадратичной скорости, определённой по теории Д-Л (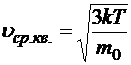 ), то есть заведомо заниженной по сравнению с тем, что должно быть при линейной температурной зависимости, экспериментальные значения r дают
), то есть заведомо заниженной по сравнению с тем, что должно быть при линейной температурной зависимости, экспериментальные значения r дают
длины свободного пробега порядка сотен межатомных расстояний.
Это полностью опрокидывает предположение II теории Д-Л.
18.4.3. Теплоёмкость металлов
Очевидно, что полная теплоёмкость металла должна складываться из теплоёмкости кристаллической решётки и теплоёмкости электронного газа:
![]() .
.
Каждый ион решётки совершает трёхмерные колебания вокруг положения равновесия, что можно представить как суперпозицию трёх одномерных осцилляторов (маятников). С энергетической точки зрения одномерный осциллятор представляет собой постоянный обмен кинетической энергии на потенциальную и обратно. В среднем на кинетическую энергию одномерного осциллятора, также как и на его потенциальную энергию приходится kT/2 тепловой энергии. Тогда на один одномерный осциллятор приходится kT тепловой энергии, а на один узел решётки приходится 3kT тепловой энергии. Для тепловой энергии одного моля решётки


