ВУЗы по физике
Готовые работы по физике
Как писать работы по физике
Примеры решения задач по физике
Решить задачу по физике онлайнПондеромоторные силы
Поскольку внутри проводника поток вектора напряжённости через любую замкнутую поверхность, из-за равенства 0 напряжённости, равен 0, то из теоремы ОГ следует, что равным 0 будет и нескомпенсированный заряд любой области внутри проводника. Следовательно,
и индуцированные, и привнесённые в проводник нескомпенсированные заряды в равновесии могут находиться только на его поверхности.
Если поверхность проводника гладкая (не имеет рёбер и острий), то для точек зрения, расположенных достаточно близко к ней, она может считаться бесконечной равномерно заряженной плоскостью с поверхностной плотностью заряда s, с одной стороны которой напряжённость поля равна 0.
Рис.16.1
По теореме ОГ легко получить, что за пределами проводника вблизи него электрическая напряжённость
,
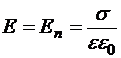где e − диэлектрическая проницаемость среды, соседствующей с проводником. Электрическое смещение на поверхности проводника:
.
На качественном уровне можно показать, что наибольшая поверхностная плотность заряда имеет место на выступах, а наименьшая − во впадинах. Изобразим эволюцию форм эквипотенциальных поверхностей при удалении от проводника без соблюдения пространственных масштабов (рис.16.2). Очевидно, что формы будут изменяться от формы поверхности проводника до сферической.
Рис.16.2
Из рисунка видно, что с удалением от поверхности проводника наиболее быстро изменение потенциала происходит около острий. Напряжённость на поверхности проводника направлена по нормали к поверхности, следовательно, равна отрицательной пространственной скорости изменения потенциала по нормальному к поверхности направлению:
.
Около острий производная 
максимальна, следовательно, максимально значение напряжённости, следовательно, максимально значение потока напряжённости через малую замкнутую поверхность S, охватывающую элемент поверхности проводника dSпов (рис.16.3). Следовательно, максимально значение охваченного заряда dQпов. Следовательно, около острий максимальна поверхностная плотность заряда 
.
§16.3. Пондеромоторные силы
Взаимодействие зарядов, сосредоточенных на поверхности проводника, приводит к возникновению сил, стремящихся эту поверхность разорвать. Эти силы называются пондеромоторными.
Рассмотрим (рис.16.4) элемент поверхностного заряда проводника 
. Этот заряд находится в поле всех остальных зарядов поверхности, характеризуемом напряжённостью 
, и испытывает на себе воздействие силы 
. Общее поле в точке нахождения заряда создано и окружением этого заряда, и самим зарядом:
,
где 
− поле самого заряда. «На взгляд» окружения место, где находится 
, − точка. С точки зрения самого заряда − бесконечная плоскость.
Рис.16.4
Внутри проводника
.
За пределами:
,
следовательно,
.
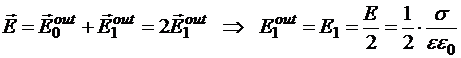Тогда сила, действующая на элемент поверхности со стороны окружения (пондеромоторная сила)
.
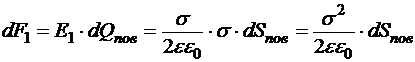Отсюда получается поверхностная плотность пондеромоторных сил:
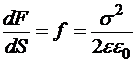
И, обозначая нормаль символом 
, можем записать поверхностную плотность пондеромоторных сил в векторном виде:
.
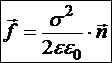Рис.16.5
§16.4. Электрическая ёмкость уединённого проводника
Уединённым называется проводник в отсутствие свободных зарядов. Для него справедливо утверждение, которое мы примем без доказательства, ограничиваясь аргументами, приведёнными в §16.2. Распределение заряда по поверхности проводника зависит только от его формы и размеров, следовательно, отношение 
не зависит от заряда проводника Q.
Для данного уединённого заряженного проводника относительная поверхностная плотность является функцией от расположения на поверхности. Рассмотрим функцию положения на поверхности этого проводника:
,
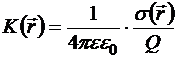где e − диэлектрическая проницаемость среды, в которую погружён заряженный проводник. Выберем произвольную точку А на поверхности проводника или внутри него. В соответствие с принципом суперпозиции потенциал этой точки можно выразить так:
,
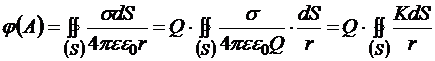где r − расстояние от текущей точки поверхности до точки А. Как видно, этот интеграл зависит только от формы, размеров данного проводника и от диэлектрических свойств его окружения. Поскольку потенциал всех точек проводника одинаков, то этот интеграл одинаков для любой точки проводника. Назовём его обратной электрической ёмкостью уединённого проводника С-1. В результате, мы получили следующее утверждение:
потенциал уединённого проводника прямо пропорционален заряду на нём.
Коэффициент пропорциональности называется обратной электрической ёмкостью уединённого проводника и не зависит ни от заряда проводника, ни от его потенциала.
Определение: электрической ёмкостью уединённого проводника (его собственной электроёмкостью) называется отношение заряда проводника к его потенциалу
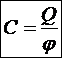
Электрическая ёмкость уединённого проводника зависит только от формы, размеров данного проводника и от диэлектрических свойств его окружения.
Расчёт электроёмкости проводника произвольной формы довольно сложен. Легко получить её выражение можно только в случае сферической формы. Из-за сферической симметрии распределение заряда по поверхности будет однородным. Следовательно, мы получаем случай равномерно заряженной сферы. Поэтому
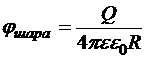Þ 
Общее правило, которое можно проследить на примере шара таково: чем больше линейный размер проводника в ряду подобных объёмных фигур, тем больше его ёмкость.
§16.5. Неуединённый проводник
Очевидно, что неуединённым называется проводник, вблизи которого находятся свободные заряды. Поскольку в электростатике внутренность проводника «не работает», то полый проводник по своим электростатическим свойствам полностью совпадает со сплошным проводником той же формы и размеров. В случае полого проводника свободные заряды могут находиться как за пределами, так и внутри него.
Качественно ситуация неуединённого проводника отличается от уединённого тем, что распределение заряда по проводнику контролируется не только формой и размером самого проводника, но и распределением в пространстве свободного заряда, не зависящим от проводника. Количественно мы будем рассматривать только случай сферического проводника и точечного свободного заряда, поскольку существует метод, позволяющий легко провести количественный анализ такой системы. Он называется методом зеркальных изображений.
МГМИМО
Скидка 30% по промокоду Diplom2020
Получи промокод на скидку 20%
Написать дипломную работу