Сила Ампера
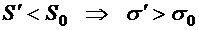 .
.
Но раз магнитное поле возникает в качестве компенсации релятивистского изменения напряжённости электрического поля, то оно должна быть очень мало при малых скоростях. Рассмотрим два движущихся в одном направлении с одинаковой скоростью заряда q1 и q2, находящихся на расстоянии r. Как известно из электростатики,
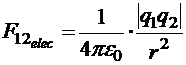 .
.
Как будет объяснено ниже,
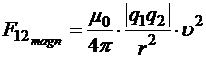 ,
,
где m0 — магнитная постоянная, u — модуль скорости зарядов. Следовательно,
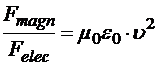
Оказывается, что 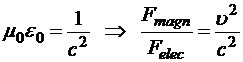 (с — скорость света в вакууме). Значит, магнитные силы, действительно, значительно меньше кулоновских. Их проявление во взаимодействии тел заметно, поскольку у реальных макроскопических тел нескомпенсированный заряд редко бывает макроскопическим, а макроскопические токи, на которые воздействует магнитное поле, в них протекают без нарушения электронейтральности.
(с — скорость света в вакууме). Значит, магнитные силы, действительно, значительно меньше кулоновских. Их проявление во взаимодействии тел заметно, поскольку у реальных макроскопических тел нескомпенсированный заряд редко бывает макроскопическим, а макроскопические токи, на которые воздействует магнитное поле, в них протекают без нарушения электронейтральности.
§19.3. Сила Ампера
Зная выражение магнитной составляющей силы Лоренца, легко вывести выражение для магнитной силы, действующей на элементарный объём проводника с электрическим током, помещённый во внешнее магнитное поле.
В элементе объёма dV находится dN=n×dV носителей заряда. Поскольку, все носители обладают общей скоростью ![]() (тепловое движение не рассматриваем, так как из-за хаотичности полная сила, связанная с ним, равна 0), то на каждый носитель действует одна и та же сила со стороны внешнего магнитного поля. Общая сила, действующая на объём dV, равна сумме всех отдельных сил, то есть
(тепловое движение не рассматриваем, так как из-за хаотичности полная сила, связанная с ним, равна 0), то на каждый носитель действует одна и та же сила со стороны внешнего магнитного поля. Общая сила, действующая на объём dV, равна сумме всех отдельных сил, то есть
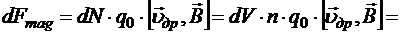
![]() .
.
В качестве dV рассмотрим элемент однородного проводника с сечением S и длиной dl в направлении вектора плотности тока ![]() (рис.19.3).
(рис.19.3).
 Рис.19.3
Рис.19.3
![]()
![]() .
.
Сила, действующая со стороны внешнего магнитного поля на проводник с током, называется силой Ампера. Следовательно, мы получили выражение элементарной силы Ампера:
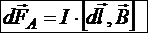 .
.
Если имеем прямой проводник конечной длины l в однородном магнитном поле, то на него действует сила Ампера
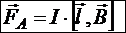 ,
,
где ![]() — вектор длины, ориентированный по току.
— вектор длины, ориентированный по току.
§19.4. Магнитный момент и воздействие на него магнитного поля

 Рис.19.4
Рис.19.4
Рассмотрим самый простой случай прямоугольной рамки с током I, со сторонами а и b в однородном магнитном поле ![]() (рис19.4). Для простоты пусть сторона а перпендикулярна
(рис19.4). Для простоты пусть сторона а перпендикулярна ![]() . Орт
. Орт ![]() — нормаль рамки, сориентированная в соответствие направлению протекания тока по правилу правого винта. Из рисунка легко понять соотношения сил, действующих на стороны рамки со стороны внешнего магнитного поля:
— нормаль рамки, сориентированная в соответствие направлению протекания тока по правилу правого винта. Из рисунка легко понять соотношения сил, действующих на стороны рамки со стороны внешнего магнитного поля: 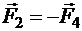 и действуют по одной прямой, оказывая на рамку растягивающее воздействие.
и действуют по одной прямой, оказывая на рамку растягивающее воздействие.
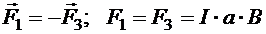 .
.
Эти силы не будут лежать на одной прямой до тех пор, пока угол a¹0. Следовательно, они будут оказывать не растягивающее, а ориентационное воздействие. Суммарная магнитная сила, действующая на рамку равна 0, значит, рамка будет вращаться вокруг неподвижной оси, проходящей через середины сторон b. Вращающий момент
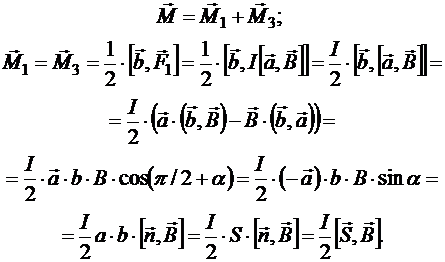
Здесь 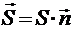 — вектор площади рамки. В результате:
— вектор площади рамки. В результате:
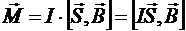 .
.
Введём определение магнитного момента плоского контура с током:
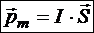 ,
,
где I — ток в контуре, ![]() — вектор площади контура, направленный по правилу правого винта в соответствие с направлением тока.
— вектор площади контура, направленный по правилу правого винта в соответствие с направлением тока.
Таким образом, на простом примере получено общее правило для определения вращающего момента, действующего на контур с током в магнитном поле:
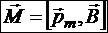
Элементарная работа магнитного поля по изменению ориентации магнитного момента:
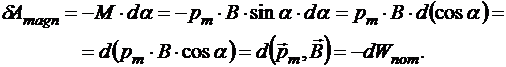
Минус в первом равенстве имеет место, поскольку воздействие вращающего момента направлено на уменьшение угла a. Последнее равенство имеет место, поскольку энергия ориентации является потенциальной, и вращающий момент — это момент потенциальных сил, работа которых направлена на уменьшение потенциальной энергии. Из него следует, что потенциальная энергия ориентации магнитного момента в магнитном поле при 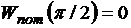 имеет вид:
имеет вид:
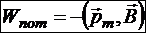
§19.5. Магнитное поле движущегося заряда
До сих пор мы рассматривали воздействие магнитного поля на движущиеся заряды. Теперь перейдём к рассмотрению магнитных полей, создаваемых ими.
 Рис.19.5
Рис.19.5
Выражение для магнитного поля движущегося точечного заряда в вакууме (рис.19.5) было получено путём обобщения опытных фактов.
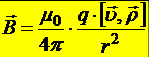 .
.
Здесь 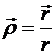 — радиальный орт,
— радиальный орт, ![]() единиц СИ — магнитная постоянная вакуума.
единиц СИ — магнитная постоянная вакуума.
§19.6. Магнитное взаимодействие зарядов
Пусть ![]() — магнитная индукция поля, созданного 1-м зарядом на месте второго. Тогда магнитная сила, с которой первый заряд воздействует на второй:
— магнитная индукция поля, созданного 1-м зарядом на месте второго. Тогда магнитная сила, с которой первый заряд воздействует на второй:
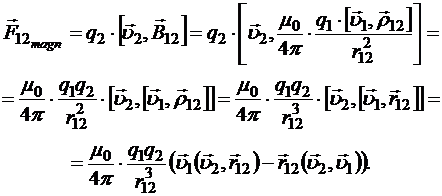
Аналогично выражение силы, с которой второй заряд воздействует на первый:
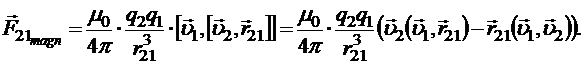
Анализ этих формул показывает, что две частицы одного заряда, движущиеся параллельно и лежащие на одной прямой, перпендикулярной их скоростям, притягиваются в соответствие с III-им законом Ньютона (рис.19.6).
 Рис.19.6
Рис.19.6
Разноимённые заряды в такой ситуации будут отталкиваться в соответствие с III-им законом Ньютона.


