Действительная характеристика центробежного наоса

β2=90о

β2>90о

Рис. 10.6

Эти характеристики представлены на рис. 10.7.

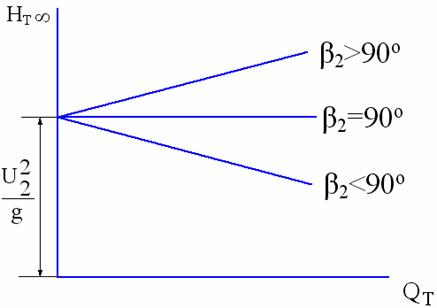
Рис.10.7

Установлено, что оптимальными к. п.д. обладают рабочие колеса, у которых угол наклона лопастей на выходе β2=14-50о, т. е. значительно меньше 90о.

10.1.5. Действительная характеристика центробежного наоса

В предыдущем разделе мы рассматривали работу по сути дела идеального центробежного насоса, т. е. насоса с бесконечно большим числом лопастей и коэффициентом полезного действия, равным единице.

Чтобы приблизиться теперь к рабочему процессу реального насоса, отбросим сначала первое из принятых допущений, оставив в силе второе, т. е. число лопастей конечное.

Обычно на практике число лопастей составляет от шести до двенадцати. В этом случае относительное течение в межлопастных каналах колеса уже не является таким струйным, как предполагалось ранее, и поэтому приводит к потере напора (1) (рис.10.8).

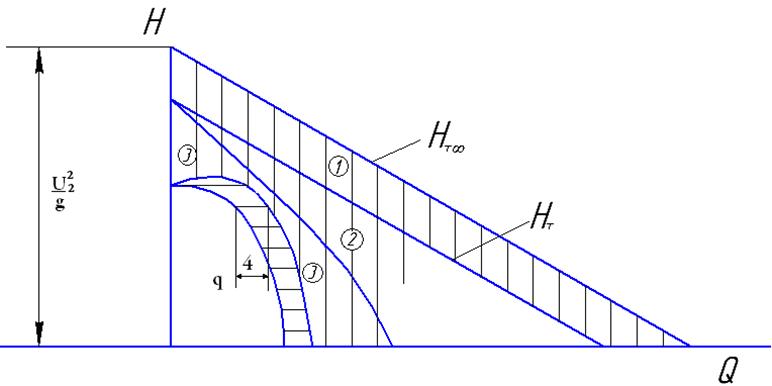
Рис. 10.8

При работе насоса с конечным числом лопастей происходят гидравлические потери (2), которые из-за турбулизации жидкости пропорциональны скорости во второй степени.

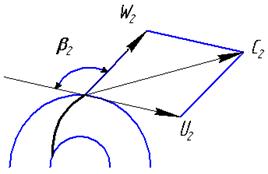
Центробежный насос спроектирован и изготовлен с таким расчетом, что максимальное значение его к. п.д. соответствует оптимальной подаче Qопт. Это означает, что относительная скорость на входе в рабочее колесо W1 касательна к кривизне лопасти. Этим обеспечивается безударный вход жидкости в рабочее колесо. Работа насоса при Qопт может осуществляться только случайно. При эксплуатации же реальная подача Qопт< Q< Qопт и поэтому удар на входе неизбежен. Это видно из параллелограммов скоростей (рис.10.9).

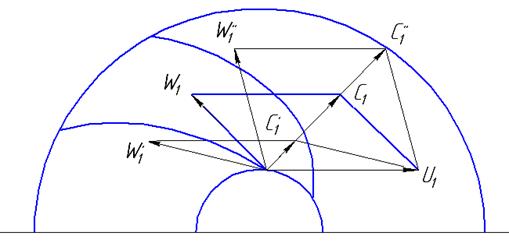
Рис. 10.9

На рис.10.8 потери на удар обозначены позицией 3.

В реальном насосе происходит утечка жидкости (4) из области высокого давления в область низкого. утечки приводят к сдвигу кривой напоров влево на величину утечек q.

Таким образом, действительная характеристика насоса имеет вид кривой второго порядка.

Приведенные выше рассуждения являются приближенными, так как они не учитывают ряд факторов, влияющих на напор и мощность. Поэтому характеристики на основании описанных рассуждений плохо согласуются с данными опыта. Действительная характеристика насоса может быть получена лишь опытным путем на основании его стендового испытания. При этом, кроме характеристики Н = f(Q), получают еще N = f(Q), = f(Q) и = f(Q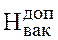) при частоте вращения n.

Характер указанных зависимостей представлен на рис. 10.10. в результате анализа этих зависимостей можно составить полное представление о работе насоса и произвести его подбор для конкретных условий.

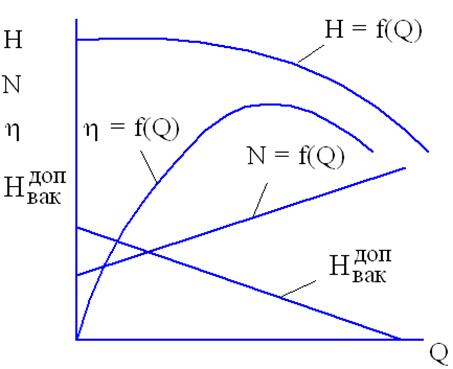
Рис. 10.10

10.1.6. Универсальные характеристики центробежного насоса

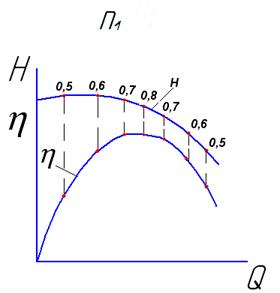
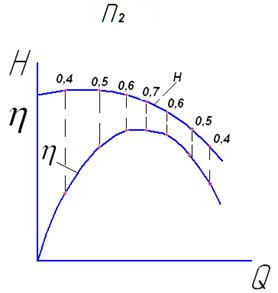
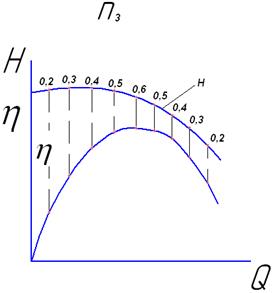
Для уточнения оптимальной частоты вращения насоса определенной серии производят его испытания при различных частотах вращения рабочего колеса, например, при n1, n2 и n3 с построением зависимостей Н = f(Q) и =f(Q) и переносом к. п.д. на кривые зависимостей Н = f(Q) (рис.10.11). Затем на один график переносят кривые Н = f(Q) с отметками значений к. п.д.

Рис. 10.11

Одинаковые значения к. п.д. соединяют тонкими линиями подобно горизонталям на топографических картах (рис.10.12).

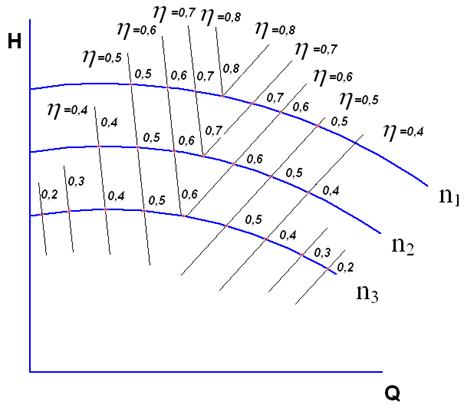
Рис. 10.12

10.1.7. Процесс всасывания и явление кавитации

в центробежном насосе

Рассмотрим наиболее распространенный случай работы центробежного насоса, когда он установлен выше уровня жидкости, находящейся под атмосферным давлением (рис. 10.13).

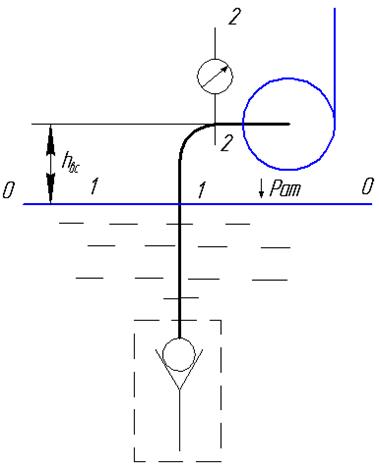
Рис. 10.13

Расстояние по вертикали от поверхности жидкости до оси насоса называют высотой всасывания hвс.

Составив уравнение Бернулли для сечения 1-1, взятого по поверхности жидкости, и сечения 2-2 на входе, где установится давление ниже атмосферного, относительно плоскости сравнения 0-0, совпадающего с сечением 1-1.

Расчетная форма уравнения Бернулли для потока реальной жидкости, как известно, имеет вид

.

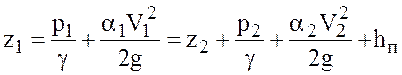После его анализа для выбранных сечений это уравнение можно записать в виде

,

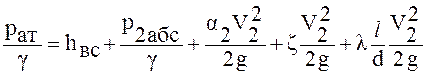где ζ – суммарный коэффициент местных потерь (обратный клапан, сетка, различные повороты и т. д.).

Выполним элементарное преобразование:

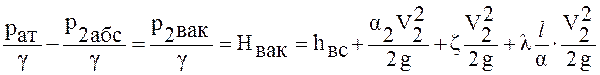. (10.8)

Когда абсолютное давление на входе в насос становится меньше или равным давлению насыщенного пара (р2 абс ≤ ) перекачиваемой жидкости, что соответствует предельно допустимому вакууму (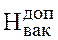), жидкость мгновенно вскипает, т. е. превращается в пузырьки пара. Перемещаясь далее в межлопастном пространстве к периферии рабочего колеса, они конденсируются ввиду повышения давления. Процесс образования пузырьков и их конденсации называется кавитацией (от латинского «каверна», что означает «пустота»). В рассматриваемом случае кавитация будет гидродинамической. Скоростной киносъемкой (2 млн 250 тыс. кадров в секунду) установлено, что в течение 1 с на площади лопасти 1 см2 образуется порядка 30·106 пузырьков.

В момент конденсации пузырька происходит местное повышение давления (до 3500 атмосфер) и температуры (1000-1200º С), и если пузырек задерживается на лопасти, произойдет ее разрушение. В разрушении участвует один из 30·103 образовавшихся пузырьков. Материалов, сопротивляющихся разрушению, практически не существует. В меньшей степени сопротивляются чугун и обыкновенные стали, в большей – титановые сплавы, высоколегированные стали. Причиной столь разрушительного действия лопнувшего пузырька является то, что в момент конденсации (время составляет 0,001 с) образуется кумулятивная микроструйка.

Кавитация сопровождается характерным шумом и треском внутри насоса, понижением к. п.д. насоса, напора и может вызвать вибрацию агрегата. Поэтому кавитация при работе насосов недопустима.

Перепишем выражение (10.8) для критического случая, когда Нвак = :

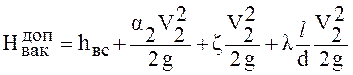. (10.9)

Из выражения (10.9) можем определить максимально возможную высоту установки насоса над поверхностью жидкости, т. е. высоту всасывания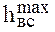

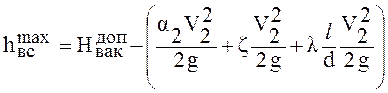(10.10)

Значение 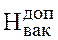берется из характеристик насоса (рис. 10.10) в зависимости от подачи Q.

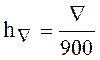Так как зависимость построена для нормального атмосферного давления (соответствующего уровню Балтийского моря) и температуры воды при 20оС, то в выражении (10.10) необходимо сделать соответствующие поправки: и ht.