Использование уравнения эйнштейна для фотоэффекта

Как следует из решения этой задачи, электромагнитная волна переносит не только энергию, но и импульс. Плотность потока энергии равна произведению плотности потока импульса на скорость света.

2.2 Использование уравнения Эйнштейна для фотоэффекта

Задача 4 [Квант 1993, 6.11]. Какую максимальную скорость могут получить вырванные из калия электроны при облучении его светом с длиной волны 400 нм? Красная граница для фотоэффекта у калия равна 550 нм.

Решение. Из соотношения Эйнштейна
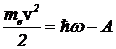, (3)
с учетом A=ћwкр, найдем
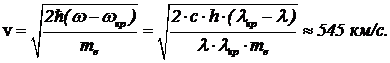(4)

В уравнении (4) использовано обозначение h=2pћ.

Задача 5 [Квант 1993, 6.12]. Некоторый металл освещается светом с длиной волны 0,25 мкм. Пренебрегая импульсом фотона, найдите максимальный импульс, передаваемый при вылете каждого электрона поверхности металла, если красная граница фотоэффекта для этого металла равна 0,28 мкм.

Задача 6 [Квант 1993, 6.13]. На один из плоских вольфрамовых электродов двухэлектродного стеклянного баллона падает пучок ультрафиолетовых лучей с длиной волны 10-7 м. На плоские электроды подано тормозящее напряжение 10 В. На каком расстоянии от первого электрода скорость фотоэлектронов уменьшится до нуля, если расстояние между электродами 40 см?

Решение. Используем результат решения задачи 5. Вылетевшие из вольфрама электроны имеют импульс 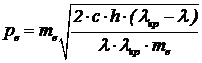. Кинетическая энергия
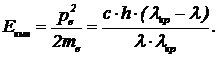. (5)

Из закона сохранения энергии для электрона, движущегося в электрическом поле, имеем
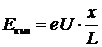, (6)
где U — напряжение на электродах, x — расстояние от первого электрода до точки остановки, L — расстояние между электродами. Уравнения (6) и (7) совместно дают
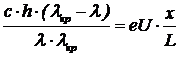, (7)
откуда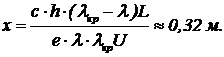
(8)

Задача 7 [Квант 1993, 6.14]. Пучок ультрафиолетовых лучей с длиной волны 10-7 м сообщает металлической поверхности мощность 10-6 Вт. Определите силу возникшего фототока, если фотоэффект вызывают 1% падающих фотонов.

Вопрос 1. Какие примеры взаимодействия света с веществом, кроме фотоэффекта, вы можете привести?

3. Домашнее задание

3.1 Теоретический материал

Повторить по пособию материал занятия 1.7.2. Дополнительно по учебнику Мякишева Г. Я., Буховцева Б. Б. “Физика 11”. §§69 -71.

4.2 Решение задач

Задача 1 [Маковецкий]. Пустотелый шарик с внутренним диаметром
1 мм с абсолютно отражающей внутренней поверхностью и абсолютно прозрачным воздухом заполнен светом с длиной волны 555 нм, так что освещенность внутри равна 200 люкс (хорошая освещенность рабочей комнаты). Во сколько раз уменьшится освещенность внутри шара, если его диаметр увеличить до 30 см? Освещенность в 1 люкс равна 1/683 Вт/м2.

Задача 2 [Квант 1993, 6.8]. Пучок лазерного излучения мощностью
100 Вт падает на непрозрачную пластинку под углом 60о. Пластинка поглощает 50% падающей энергии, а остальную часть зеркально отражает. Найдите силу светового давления.

Задача 3. Фотоэффект вызывается рентгеновским излучением с длиной волны 10-12 м. С какой максимальной скоростью вылетают из вещества фотоэлектроны? Почему для решения задачи несущественна информация о работе выхода электронов из вещества?

занятие 2.1.4

эффект комптона

2. Рассеяние рентгеновского света

2.1 Двуединость фотона

Эксперименты по интерференции и дифракции указывают на то, что свет это электромагнитная волна. А фотоэффект указывает на то, что свет состоит из потока частиц, каждая из которых обладает кинетической энергией. Причем корпускулярная характеристика — энергия — связана с волновой характеристикой — частотой — соотношением:
E=ћw. (1)
Имеет смысл рассмотреть явление, в котором характеристики фотона как частицы проявились бы более явно, чем в фотоэффекте. Рассеяние рентгеновских фотонов на электронах является таким явлением.

2.2 Теория эффекта Комптона

Предположение о корпускулярных свойствах фотона дополним представлением о том, что фотон имеет импульс
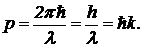(2)

Построим теоретическую картину рассеяния фотонов на электронах. Итак, фотон с энергией Eg=ћw и импульсом сталкивается с покоящимся электроном, масса которого равна me. После столкновения фотон частично передает свою энергию электрону и отражается под углом J, имея меньшую энергию 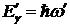и импульс . После отражения электрон приобретает энергию Ee и импульс .

Ниже следующие расчеты надо проводить учитывая, что рассеиваемые фотоны имеют энергии того же порядка, что и энергия покоя электронов. То есть, надо применять релятивистские соотношения.

При столкновении энергия и импульс сохраняются по отдельности. Начальный импульс фотона и импульсы фотона и электрона после столкновения должны лежать в одной и той же плоскости. Законы сохранения энергии и импульса можно записать так:
ћ(w-w`)+ mec2=Ee, (3)
(4)
Уравнение (3) и уравнение (4) почленно возведем в квадрат и после умножения обеих частей уравнения (4) на c2 в новом виде вычтем из первого второе:
(5)

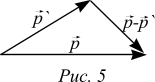
Прежде, чем продвигаться дальше, обсудим геометрический смысл слагаемого . Разность 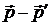в треугольнике векторов является стороной, лежащей напротив угла рассеяния J. Поэтому по теореме косинусов
(6)
Учтем, что , , 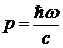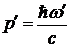и раскроем скобки в левой части уравнения (5). Тогда
-2ћ2ww`+2ћ(w-w`)mec2 +2ћ2ww`cosJ=0. (7)
Решим уравнение (7) относительно частоты рассеянного света w`. Решение дает
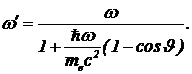(8)

Частота рассеянного света оказывается меньшей частоты падающего света. Это согласуется с ожиданием уменьшения энергии налетающего фотона вследствие передачи части энергии электрону. Как видно, изменения не происходит при J=0 и максимальное изменение частоты происходит при J=p.

Задача 1. Определите, чему равно относительное изменение частоты фотона рассеянного на электроне в противоположную сторону первоначальному направлению распространения.

Решение. Угол рассеяния равен p. После подстановки данного значения угла в формулу (8) получим: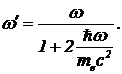
(9)
Изменение частоты w—w` равно
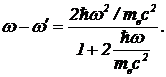. (10)
Относительное изменение частоты равно
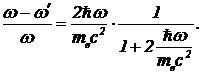(11)