Ламинарное и турбулентное течение жидкости

Единицей измерения вязкости в СИ является . Вязкость зависит от природы жидкости и температуры. Она может быть измерена с помощью специальных приборов, которые называются вискозиметрами. Часто ограничиваются определением относительной вязкости жидкости, которая равна отношению ее вязкости к вязкости воды.

Ньютоновские и неньютоновские жидкости

Не для всех жидкостей можно описать силу трения с помощью уравнения Ньютона. Это уравнение применимо лишь к тем жидкостям, вязкость которых определяется только их природой и температурой и не зависит от скорости их течения. К этой категории относятся однородные низкомолекулярные жидкости (вода, спирт и т. д.) Жидкости такого рода называются ньютоновскими. Уравнение Ньютона неприменимо к жидкостям, неоднородным по своему составу. К ним относят суспензии, эмульсии, пены и также растворы веществ, состоящих из крупных молекул, имеющих форму длинных цепочек. Такие жидкости называются неньютоновскими.

Реологические свойства неньютоновских жидкостей зависят от деформируемости и прочности, входящих в них структурных элементов, от особенностей их движения, способности объединяться в агрегаты. Присутствие в жидкости взвешенных частиц или других включений изменяет картину течения жидкости. Поэтому вязкость неньютоновских жидкостей зависит не только от их природы и температуры, но и от градиента скорости их течения.

Ламинарное и турбулентное течение жидкости

Ламинарным называется такое течение жидкости, при котором она перемещается как бы слоями, каждый из которых характеризуется своей скоростью.

Именно такой вид течения был представлен на рис.6. При ламинарном течении жидкости в трубке круглого сечения она движется как бы коаксиальными цилиндрическими слоями, и все ее частицы перемещаются только параллельно оси трубки. Скорость течения максимальна в центре сечения трубки и уменьшается по направлению к ее стенками. Профиль распределения векторов скоростей в такой трубке показан на рис.7. Он представляет собой параболу.

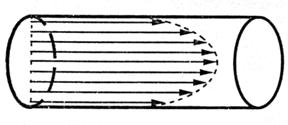
Рис. 7 Профиль распределения векторов скоростей жидкости

при ламинарном течении

Возможен и другой тип течения жидкости — турбулентное. При турбулентном течении скорости частиц жидкости беспорядочно меняются, в результате чего в потоке образуются местные завихрения, и ее частицы перемещаются не только параллельно, но и перпендикулярно оси трубки. В этих условиях происходит непрерывное перемешивание частиц жидкости.

Рейнольдс показал, что переход ламинарного течения жидкости в турбулентное зависит от ряда величин: вязкости жидкости , ее плотности , скорости ее течения v и диаметра трубки D, Эти величины входят в уравнение Рейнольдса:

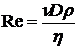
Re — безразмерная величина, так называемое число Рейнольдса. При малых значениях этого числа течение жидкости является ламинарным. Когда число Рейнольдса превышает некоторую критическую величину, ламинарное течение превращается в турбулентное. Для трубки круглого сечения такая величина числа Рейнольдса составляет примерно 2000.

Течение вязкой жидкости по трубкам. Уравнение Пуазейля

.
Хаген, изучая течение воды по трубкам, показал, что ее объемная
скорость пропорциональна четвертой степени радиуса трубок. Более подробно
исследовал это явление Пуазейль — автор важнейших работ по гидродинамике и физиологии кровообращения. Он установил экспериментально закон, характеризующий величину объемной скорости жидкости Q в трубках круглого сечения, и представил его в виде соответствующего уравнения, которое называют также основным уравнением гидродинамики.

Пусть жидкость, обладающая вязкостью , течет по трубке с радиусом r (рис.8). Для того, чтобы определить ее объемную скорость Q , необходимо измерить разность давлений (полных) Р1 и Р2 на участке трубки длиной l.

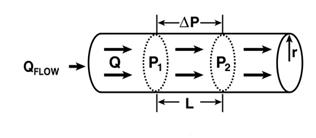
Рис. 8. Факторы, определяющие объемную скорость жидкости.

Величина объемной скорости Q определяется уравнением Пуазейля:

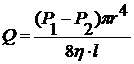
В соответствии с уравнением Пуазейля, объемная скорость
жидкости в трубке определяется разностью давлений в начале и конце трубки,
зависит от четвертой степени радиуса, а также от длины трубки и вязкости
жидкости:

Уравнение Пуазейля можно упростить и в то же время сделать его более универсальным, если ввести дополнительную величину R — гидродинамическое сопротивление:

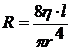
Тогда уравнение Пуазейля примет вид: 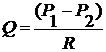, или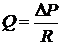

Использование понятия гидродинамического сопротивления расширяет рамки применения уравнения Пуазейля от единичной трубки круглого сечения до системы любой сложности, состоящей из многих трубок, соединенных последовательно или параллельно. Если не во всех случаях можно рассчитать гидродинамическое сопротивлении такой системы, то его можно, по крайней мере, измерить экспериментально.

Таким образом, смысл уравнения Пуазейля сводится к тому, что объемная скорость жидкости находится в прямой зависимости от разности давлений в начале и в конце трубки или системы трубок и в обратной зависимости от величины гидродинамического сопротивления.

Записанное в такой форме уравнение Пуазейля напоминает закон Ома для постоянного электрического тока. При этом объемная скорость жидкости аналогична силе тока, разность давлений — разности электрических потенциалов на концах проводника, а гидродинамическое сопротивление — электрическому сопротивлению. Это обстоятельство позволяет моделировать с помощью электрических цепей течение жидкости в трубках, в частности течение крови в сосудистой системе.

Необходимо отметить, что уравнение Пуазейля применимо только к ламинарному течению жидкости. В турбулентном потоке происходит более значительная убыль энергии, чем в ламинарном. Поэтому если развивается турбулентность, объемная скорость жидкости перестает отвечать уравнению Пуазейля. Ее величина становится приблизительно пропорциональной квадратному корню из разности давлений в начале и конце трубки.

Биофизические основы кровообращения

Работа сердца

При каждой систоле сердце совершает работу А по приданию определенному объему крови V (систолическому объему) статического давления Р, а также по приданию массе крови m скорости . Из этого следует, что работа как левого, так и правого желудочков сердца за один цикл составляет:

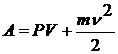
Поскольку величины Р и V меняются во времени, для получения точного значения А было бы необходимо проинтегрировать их. Однако задачу можно упростить, если взять их средние значения.

Из экспериментов известно, что средняя величина Р для левого желудочка составляет в покое приблизительно 100 мм рт. ст., а для аорты — 0,5 м/с. Величина V в покое равна в среднем 70мл. Подставив эти величины в приведенное выше уравнение, получим примерную величину работы левого желудочка за один сердечный цикл.

PV = 0,931 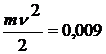Дж

Дж

А = 0,931 Дж + 0,009 Дж

Таким образом, 99% работы левого желудочка сердца затрачивается на то, чтобы повысить давление в объеме крови, изгоняемом из него, и лишь 1% — на сообщение скорости этому объему крови. Соответственно, статическое давление в аорте составляет 99% полного давления, а динамическое — только 1% . Иначе говоря, основная часть удельной энергии крови в аорте является потенциальной и лишь очень малая часть – кинетической

Давление крови в легочной артерии значительно ниже, чем в аорте, а скорость крови примерно такая же. Подсчеты показывают, что для правого желудочка А = 0,15Дж.