Лекция по статике — пара сил

2. Пусть сила , приложенная в точке А, стремится повернуть тело вокруг точки О

3. Вращательный момент этой силы будет зависеть от расстояния h — от точки О до линии действия силы (и не зависеть от точки приложения силы – так как силу можно переносить по линии её действия)

4. Момент силы относительно точки (центра О) называется величина = сила ×на кратчайшее расстояние: от точки О до линии действия силы с соответствующим знаком.

5. Правило знаков:

А) знак «+» — момент (изгиб) силы, которая стремится повернуть тело вокруг точки О против хода часовой стрелки.

Б) знак «-» — по ходу часовой стрелки.

В) если линия действия силы проходит через точку, то момент силы относительно этой точки = нулю.

6. Плечо относительно центра О – перпендикуляр из точки О на линию действия силы

Пара сил

1. Пара сил — система двух сил, приложенных к телу в двух разных точках:

— равных по модулю

— параллельных

— противоположно направленных

2. Плечо пары сил – кратчайшее расстояние между линиями действия сил пары.

Момент пары сил

Момент пары сил — произведение модуля любой силы на плечо пары (модуль силы х плечо)

Свойства пары сил

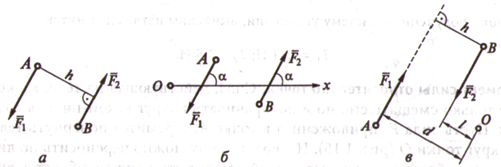
1. Сумма проекций на любую ось сил пары равна нулю

F2cosα – F1cosα = 0

2. Сумма моментов сил пары относительно любой точки плоскости равна моменту пары.

momo() = — F1d = — Fd

momo() = + F2l = +Fl

momo() + momo() = — Fd + Fl = — F(d-l) = — Fh

Следовательно, пару сил нельзя заменить равнодействующей.

Самостоятельная работа обучающегося по теме 1.3. (1 час – все)

1. Составить глоссарий основных понятий по теме «Пара сил» — арх, ‘эзс – 1 час

1. Решение задач на определение моментов сил относительно точки: авто – 1час

ТЕМА 1.4. ПЛОСКАЯ СИСТЕМА ПРОИЗВОЛЬНО РАСПОЛОЖЕННЫХ СИЛ

– (4 час арх, 2час авто, эзс)

Основные понятия

1. Плоская система сил – система сил, линии действия которых лежат в одной плоскости.

2. На плоскости могут быть приложены силы:

А) произвольно расположенные;

Б) пары сил;

В) силы, сходящиеся в одной точке.

3. Плоская система произвольно расположенных сил – все силы или линии их действия не пересекаются в одной точке.

Приведение плоской системы сил к заданному центру

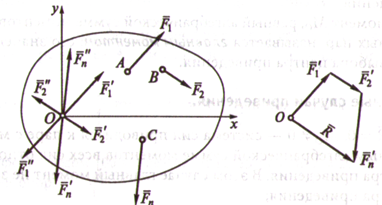
1. Пусть на твёрдое тело действует система сил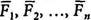

2. Приложим в точке О по 2 уравновешенные силы:

А) одна равна и параллельна заданной:

Б) другая сила равна заданной, но противоположно направлена

3. В итоге на тело действует:

А) система сходящихся сил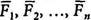

Б) система пар сил с моментами

4. Систему сходящихся сил заменяем равнодействующей

Или в соответствии с тем, что и т. д.

5. В соответствии со вторым свойством пары сил найдём алгебраическую сумму моментов всех пар

Мо = m1 + m2 + …+ mn

Лемма Пуансо

1. В результате произвольную плоскую систему сил можно заменить:

— одной силой, равной геометрической сумме всех сил, приложенных в произвольно выбранном центре и

— моментом, равным алгебраической сумме моментов присоединенных пар

2. Принятые определения:

А) точка о – центр приведения

Б) главный вектор – вектор R, равный геометрической сумме всех сил. Его значение не зависит от выбора центра приведения.

В) главный момент – момент МО, равный алгебраической сумме моментов присоединённых пар. Его значение зависит от выбора центра приведения (величина плеча будет меняться).

Частные случаи приведения

1. R0=0,M0≠0 – система эквивалентна паре сил с моментом, равным главному моменту системы, который в этом случае не зависит от выбора центра приведения;

2. R0≠0,M0=0 – система эквивалентна равнодействующей R. Главный вектор в данном случае – является равнодействующей.

3. R0≠0,M0≠0 – система эквивалентна равнодействующей R, приложенной в новом центре приведения, расположенном от прежнего на расстоянии d = МоR

4. R=0,M0=0 – плоская система сил находится в равновесии;

Теорема Вариньона (о моменте равнодействующей плоской системы сил)

Момент равнодействующей плоской системы сил относительно произвольного центра О равен алгебраической сумме моментов всех сил системы относительно этого центра.

Аналитические уравнения равновесия плоской системы сил

Условие равновесия выражается тремя уравнениями – основные уравнения равновесия:

2. Варианты записи уравнений равновесия – в зависимости от расположения сил

или

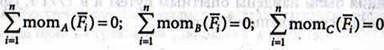
Класссификация нагрузок

Сосредоточенная Распределённая: по линии, по поверхности, по объёму Изгибающий момент

Балочные системы

1. Объект решения задач статики – балки (или балочные системы)

2. Балка – деталь в виде прямого бруса с опорами в двух (или более) точках.

Виды опор

1. Шарнирно-подвижная: вращение вокруг своей оси (шарнир) + поступательное перемещение (подвижная)

2. Шарнирно-неподвижная: вращение вокруг своей оси (шарнир)

3. Жёсткая заделка (защемление): препятствует любому перемещению.

Решение задач на определение опорных реакций

С помощью трёх уравнений равновесия определяют реакции опор (если число реакций связи не превышает трёх):

1. Показать нагрузки

2. Обозначают нагрузки

3. Освобождаются от опор и заменяют их действие на балку реакциями

4. Составляют уравнение равновесия

5. Решают уравнения равновесия и определяют из них опорные реакции

6. Проверка решения

Определение усилий в стержнях плоских ферм – вырезанием узлов

1. Аналитический способ

2. Графический способ – построением диаграммы Максвелла – Кремоны

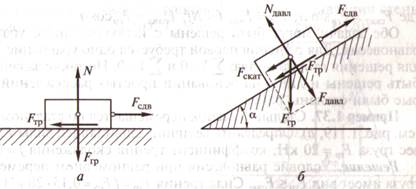
Элементы теории трения

ТЕМА 1.5. ЭЛЕМЕНТЫ ТЕОРИИ ТРЕНИЯ (авто — 1 час)

Самостоятельная работа обучающегося (авто – 1час)

1. Решение задач по индивидуальным заданиям

1. Понятие о трении

Сила трения возникает при соприкосновении тел и препятствует передвижению одного тела по поверхности другого.

2. Виды сил трения:

А) трение скольжения

Б) трение скольжения

3. Трение скольжения – сопротивление, возникающее при относительном перемещении одного тела по поверхности другого.