Несвободное твердое тело. типы связей и реакции

Принцип отвердевания.

Равновесие сил, приложенных к деформируемому телу сохраняется при отвердевании. Это только необходимое, но недостаточное условие равновесия.

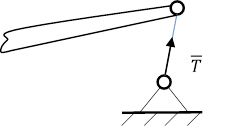
Для троса, в отличие от стержня, силы должны быть только растягивающими. Для стержня должны быть растягивающими и сжимающими.

Несвободное твердое тело. Типы связей и реакции.

Свободное тело – твердое тело, которое может перемещаться в любом направлении в пространстве.

Несвободное тело имеет ограничение в одном из возможных направлений.

Тела, которые ограничивают перемещение тела, в одном из направлений, называются связями.

Силы, с которыми связь действует на тело, называется реакциями связи.

Для определения направления и модуля используется принцип освобождаемости от связи, то есть тело считаем свободным и прикладываем к нему заданные силы и реакции связи. Сами связи на чертеже не показываем, внутренние силы не учитываются, так как уравновешиваются по свойству внутренних сил, которое выражается в том, что главный вектор и главный вектор-момент относительно любого центра приведения равны нулю.

Типы связей и реакции

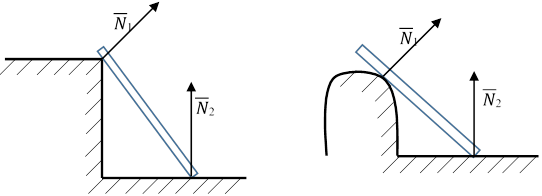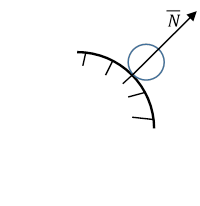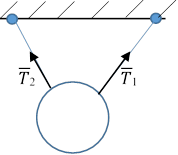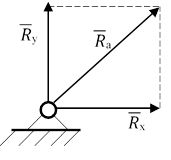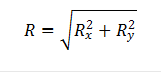
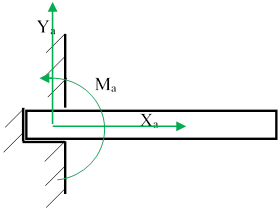
Способы задания и сложения сил.

Сходящаяся система сил.

Геометрический и аналитический методы при определении реакции связи, сходящейся системы сил

Существует два способа задания и сложения сил:

1)  геометрический;

2)  аналитический;

В первом случае сила задается ка вектор, во втором с помощью проекций на оси координат.

Рассмотрим, как складываются силы на примере сходящейся системы сил.

Сходящимися называются силы, линии действия которых пересекаются в одной точке. Эти силы могут быть в плоскости и в пространстве.

Геометрический способ

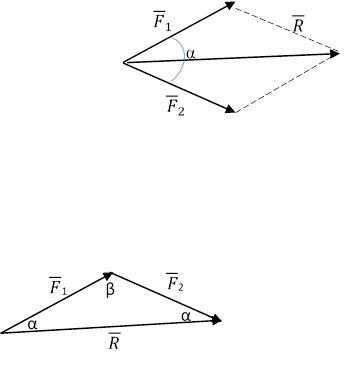
В соответствие с четвертой аксиомой, равнодействующая двух пересекающихся сил приложена к точке их пересечения и определяется как диагональ.

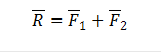
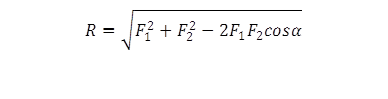Равнодействующая будет также действовать как F1 и F2. На этих силах можно построить силовой треугольник.

С помощью теоремы синусов можно найти зависимость сил.

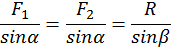
Если имеем систему сходящихся сил, то главный вектор можно определить путём последовательного сложения сил по правилу параллелограмма, но удобнее строить силовой многоугольник.

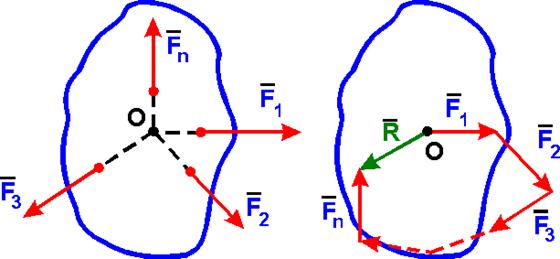
Система сходящихся сил имеет равнодействующую равную главному вектору этих сил и приложена в точке пересечения.

Из рассуждений очевидно, если силовой многоугольник замкнут, то равнодействующая равна нулю и все силы взаимно уравновешены. Это положение выражает условие равновесия сходящихся сил в геометрической форме.

Для равновесия системы сходящихся сил, приложенных к твердому телу необходимо и достаточно, чтоб равнодействующая равнялась нулю.

Аналитический способ задания и сложения сил.

Силу можно задать с помощью проекции на ось. Проекция вектора на ось – длина отрезка ab.

На плоскости:

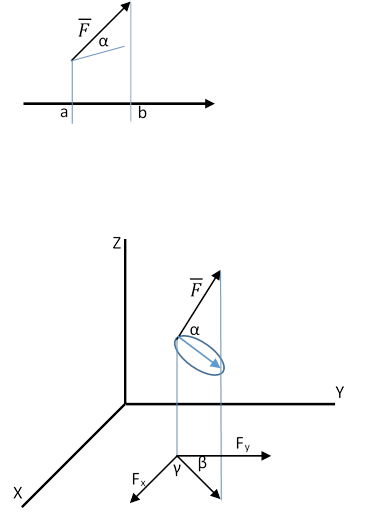
В пространстве:

Для сложения сил аналитический служит теорема «о проекции вектора суммы»:

Проекция вектора суммы на ось равна алгебраической сумме слагаемых сил на ту же ось.

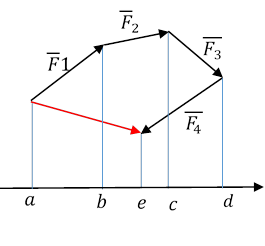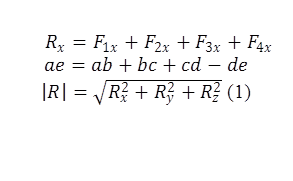Если рассматривается система сходящихся сил в равновесии, то вектор равен нулю, то есть из (1) вытекает условие равновесия:

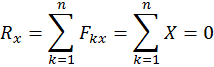
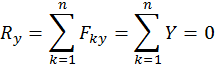
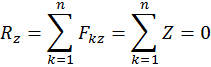
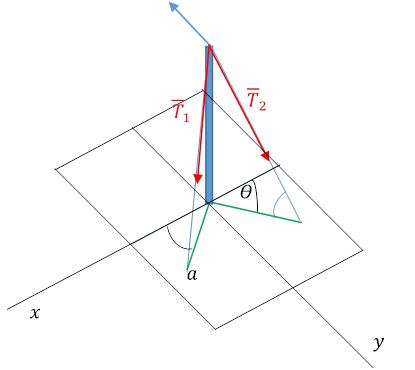
Для равновесия любой сходящейся системы сил (на плоскости или в пространстве) необходимо и достаточно, чтоб сумма проекций сил на каждую координатную ось равнялась нулю.

Если силы находятся в одной плоскости, то достаточно двух уравнений.

Составляем уравнение сходящейся пространственной системы сил.

Силы уравновешиваются. Для определения Т1, Т2, Rc используем аналитические условия равновесия.

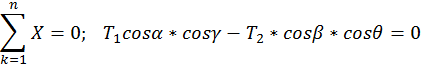
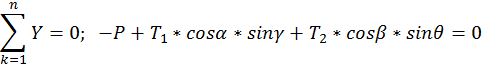
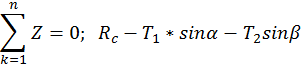
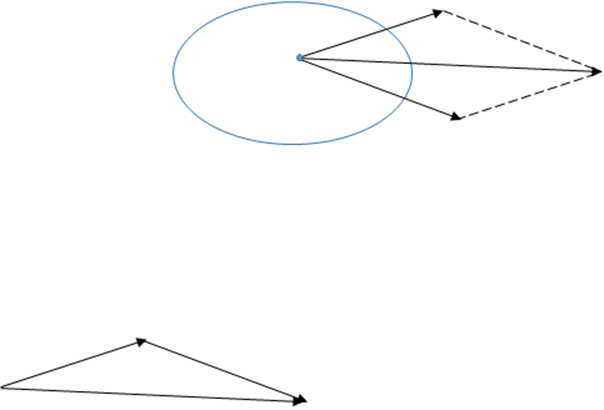
Теорема о трех силах

Если свободное твердое тело находится в равновесии под действием трех непараллельных сил, лежащих в одной плоскости, то линия этих сил пересекается в одной точке, а силовой треугольник должен быть замкнут.

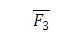
Так как тело находится в равновесии под действием трех сил, то равна и противоположна .

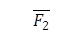
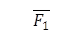
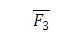При равновесии тела под действием трех сходящихся сил, из линии действия должны пересечься в одной точке.

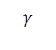
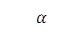
Силовой треугольник замкнут.

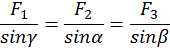
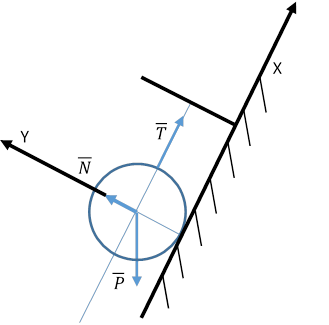Пример 1

Действуют три силы: Т, N, Р

Геометрический способ

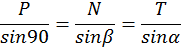
Аналитический способ

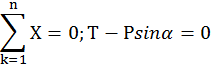
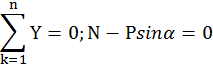
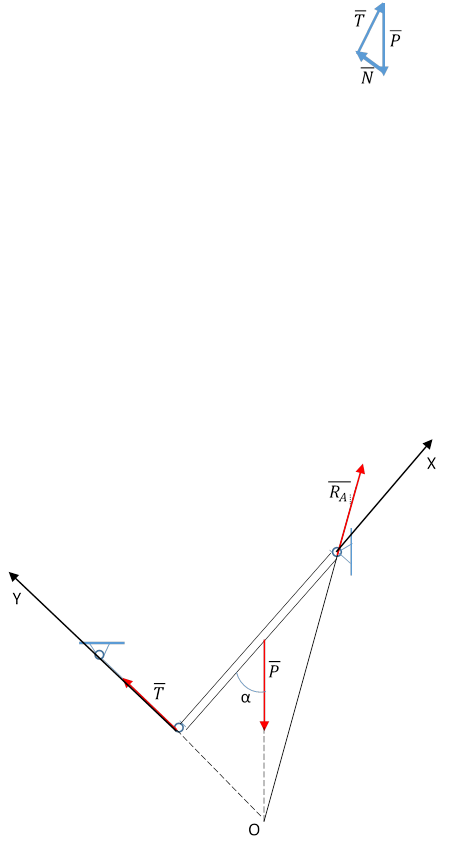
Пример 2

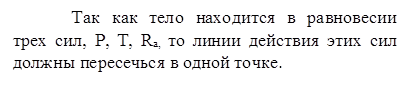
Решим задачу геометрическим способом

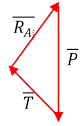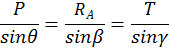
Аналитический метод решения

Составим уравнения равновесия в аналитической форме.

При решении задач данного типа применяется принцип освобождаемости от связи, то есть вместо связей указываются их реакции и нагрузки.

Если число неизвестных величин больше числа уравнений равновесия, то задача статически неопределима, а система сил называется статически неопределимой.

Момент силы.
Момент силы относительно центра и осей

Моментом силы относительно произвольного центра в плоскости действия силы, называется произведение модуля силы на плечо.

Плечо — кратчайшее расстояние от центра О до линии действия силы, но не до точки приложения силы, т. к. сила-скользящий вектор.

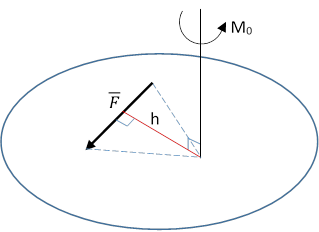Знак момента:

По часовой-минус, против часовой-плюс;

Момент силы можно выразить как вектор. Это перпендикуляр к плоскости по правилу Буравчика.

Если в плоскости расположены несколько сил или система сил, то алгебраическая сумма их моментов даст нам главный момент системы сил.

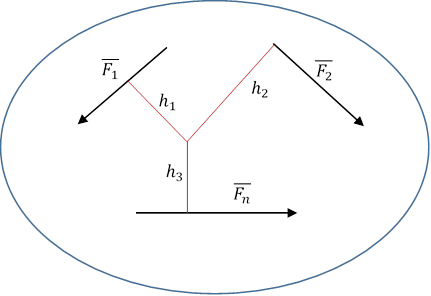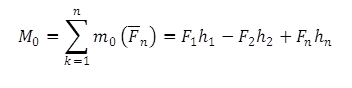
Рассмотрим момент силы относительно оси, вычислим момент силы относительно оси Z;

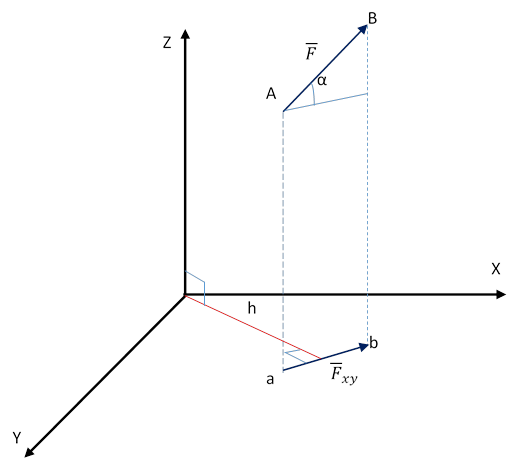Спроецируем F на XY;

Fxy=Fcosα=ab

m0(Fxy)=mz(F), то есть mz=Fxy*h= Fcosα*h

Момент силы относительно оси равен моменту ее проекции на плоскость перпендикулярную оси, взятому на пересечении осей и плоскости

Если сила параллельна оси или пересекает ее, то mz(F)=0

Выражение момента силы в виде векторного выражения

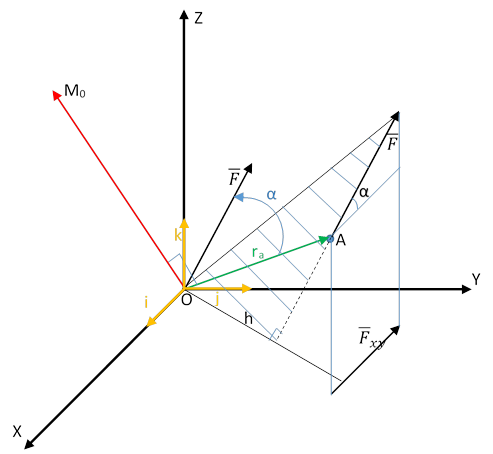Проведем rа в точку A. Рассмотрим OA x F.

Это третий вектор mo, перпендикулярный плоскости. Модуль векторного произведения можно вычислить с помощью удвоенной площади заштрихованного треугольника.

Аналитическое выражение силы относительно координатных осей.

Предположим, что с точкой О связаны оси Y и Z, X с единичными векторами i, j, k Учитывая, что:

rx=X * Fx ; ry=Y * Fy; rz=Z * Fy получим: mo(F)=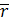 x =

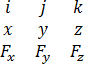
Раскроем определитель и получим:

mx=YFz — ZFy

my=ZFx — XFz

mz=XFy — YFx

Эти формулы дают возможность вычислить проекцию вектор-момента на оси, а потом и сам вектор-момент.

Теорема Вариньона о моменте равнодействующей

Если система сил имеет равнодействующую, то её момент относительно любого центра равен алгебраической сумме моментов всех сил относительно этой точки

Если приложить Q= — R, то система (Q, F1 … Fn) будет равен уравновешиваться.

Сумма моментов относительно любого центра будет равен нулю.

Аналитическое условие равновесия плоской системы сил

Это плоская система сил, линии действия которых расположены в одной плоскости

Цель расчета задач данного типа — определение реакций внешних связей. Для этого используются основные уравнения в плоской системе сил.