Нормальное напряжение в жидкости

В общем случае при движении жидкости поверхностная сила ΔR, действующая на элементарной площади Δw, направлена под некоторым углом к ней, и силу ΔR можно разложить на нормальную ΔР и тангенциальную ΔТ составляющие (рис. 1.1).

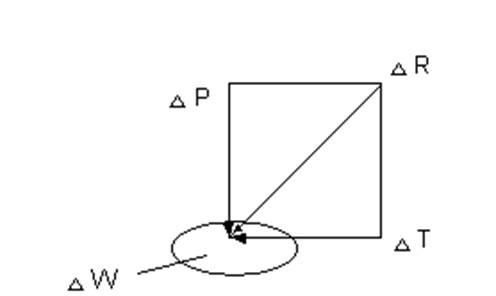
Рис. 1.1

Нормальное напряжение в жидкости называется давлением.

Истинное давление

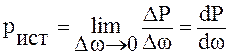. (1.1)

Среднее давление на заданной поверхности

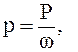Н/м2 (1.2)

Касательное напряжение в жидкости, т. е. напряжение силы трения обозначается τ и выражается подобно давлению.

Истинное касательное напряжение

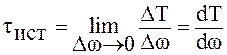. (1.3)

Среднее касательное напряжение на заданной поверхности

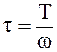, Н/м2 (1.4)

Способность жидкости воспринимать сжимающие усилия (давления) ничем не ограничена. Этого нельзя сказать о растягивающих усилиях. Наличие в жидкостях мельчайших твердых частиц и растворенного воздуха делает их практически не сопротивляющимися растяжению. Примем это утверждение за аксиому.

2. Физические свойства жидкости

2.1. Плотность и удельный вес жидкости

Ввиду того, что жидкость в отличие от твердого тела в значительно большей степени подвержена изменению своей массы под действием внешних сил, строго судить о плотности можем только в данной точке жидкости, т. е. плотностью жидкого тела будем называть предельное значение отношения массы элементарного тела к его объему. Такая плотность называется истинной

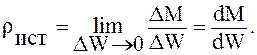(2.1)

Пренебрегая изменением массы, т. е. считая жидкость однородной, ее плотность можно выразить аналогично твердому телу, т. е.

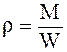, кг/м3 (2.2)

Плотность жидкостей зависит от температуры. Она уменьшается с ее ростом. Некоторым особняком в этом отношении находится вода. Так, дистиллированная вода имеет максимальную плотность, равную 1000 кг/м3 при температуре порядка 4оС. до этой температуры и после она меньше. Это имеет принципиальное значение с точки зрения обмена слоев воды в естественных водоемах.

Для удобства составления таблиц плотностей различных физических тел, в том числе и жидкостей, применяют понятие относительной плотности δ, равной плотности физического тела к плотности воды при 4оС:

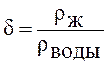. (2.3)

По аналогии с плотностью истинным удельным весом называется предельное значение отношения веса элементарного тела к его объему:

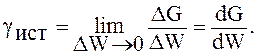(2.4)

Если считать жидкость однородной, ее удельный вес можно выразить как

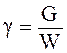, Н/м3 (2.5)

Связь между удельным весом и плотностью в земных условиях легко найти, если учесть, что G = М·g:

γ = ρg. (2.6)

Для инструментального определения плотности служат приборы, называемые ареометрами.

2.2. Сжимаемость жидкости

Сжимаемостью называют свойство жидкости обратимым образом изменять свой объем при всестороннем сжатии.

Характеризуется сжимаемость коэффициентом объемного сжатия, который представляет собой относительное изменение объема, приходящееся на единицу давления:

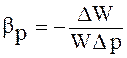, м2/Н (2.7)

Знак минус в формуле имеет символическое значение и обусловлен тем, что положительному приращению давления р соответствует отрицательное приращение (т. е. уменьшение) объема W.

Величина, обратная коэффициенту βр, представляет собой объемный модуль упругости К:

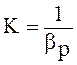, Н/м2 (2.8)

Для жидкостей модуль К несколько уменьшается с увеличением температуры и возрастает с повышением давления. Для воды он составляет при атмосферном давлении приблизительно 2000 МПа. Следовательно, при повышении давления на 0,1 МПа объем воды уменьшается всего на 1/20000 часть. Такого же порядка модуль упругости и для других жидкостей.

В большинстве случаев жидкости можно считать практически несжимаемыми, т. е. принимать их плотность не зависящей от давления. Но при очень высоких давлениях и упругих колебаниях сжимаемость жидкости следует учитывать.

2.3. Температурное расширение жидкости

Повышая температуру жидкости, мы обычно заставляем ее молекулы удаляться друг от друга. Температурное расширение характеризуется коэффициентом температурного расширения βt, который равен относительному изменению объема W при изменении температуры на один градус:

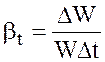, 1/град (2.9)

При нагревании жидкости в герметичном объеме в последнем повысится давление на величину Δр:

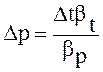, Н/м2 (2.10)

Значение коэффициента температурного расширения βt зависит от давления, действующего на рассматриваемый объем жидкости. В частности, у воды он увеличивается с возрастанием давления при повышении ее температуры от 0 до 50оС и уменьшается с возрастанием давления при дальнейшем повышении ее температуры. У большинства других жидкостей коэффициент βt уменьшается с увеличением давления при любой температуре.

При гидравлических расчетах водопроводных сооружений температурным расширением воды можно пренебречь из-за незначительного изменения температуры и давления воды, а при расчете тепловых сетей температурное расширение воды учитывают.

Для воды, например, осредненное ориентировочное значение коэффициента температурного расширения βt равно 14·10-6 1/град.

2.4. Вязкость жидкостей

При движении жидкости в трубах и открытых руслах каждый слой ее частиц скользит по другому, т. е. внутри жидкости происходит процесс, аналогичный трению. Силы, возникающие в результате скольжения слоев жидкости, называют силами внутреннего трения, или силами вязкости.

Свойство жидкости оказывать сопротивление касательным усилиям называют тангенциальной вязкостью.

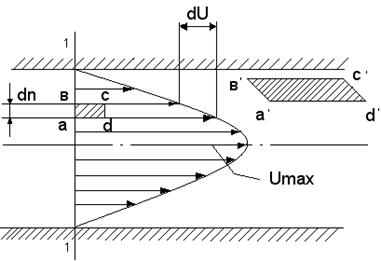
Рассмотрим движение жидкости, при котором скорости отдельных ее частиц параллельны оси трубы. Опыт показывает, что такое движение жидкости существует в природе (оно называется ламинарным и в дальнейшем будет подробно изучено). Скорости частиц, расположенных в некотором поперечном сечении трубы 1-1, отличаются друг от друга (рис. 2.1).

Скорость жидкости у стенки равна нулю, возрастает по направлению к оси трубы, достигая на оси наибольшего значения Umax. Поток жидкости может быть представлен как движение отдельных бесконечно тонких цилиндрических слоев жидкости, перемещающихся с различными скоростями, увеличивающимися к оси трубы.

Рис.2.1

Вследствие молекулярного движения молекулы жидкости пересекают слои жидкости, движущиеся по отношению друг к другу с относительной скоростью, благодаря чему на поверхности соприкасающихся слоев жидкости возникают силы трения. При этом слои жидкости, движущиеся быстрее, увлекают за собой слои, движущиеся медленнее, тормозят движение слоев, движущихся быстрее. В таком движении частицы жидкости в виде прямоугольника a, b, c, d деформируются в параллелограмм a,,b,, c,, d,. Деформация объема является обязательным условием возникновения сил трения.

Исаак Ньютон в 1687 году сумел установить, что силы внутреннего трения, возникающие между соседними движущимися слоями жидкости, прямо пропорциональны скорости относительного движения и площади поверхности соприкосновения, вдоль которых совершается относительное движение, зависят от рода жидкости и не зависят от давления.

Гипотеза Ньютона подвергалась многократной опытной проверке и полностью подтвердилась. Чрезвычайно ценные исследования для доказательства этой гипотезы были выполнены крупнейшим русским ученым, профессором Н. П. Петровым (1836-1920 гг.), создателем гидродинамической теории смазки.