Преобразования лоренца для координат и времени

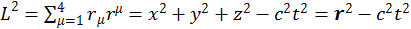(1.2.13)

Многие физики четвертую координату стали обозначать с индексом нуль и писать: 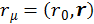, , 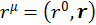µ=0,1,2,3, т. е.

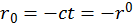(1.2.14)

Таким образом, мы имеем

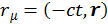(1.2.15)

Далее будем предполагать, что ковариантные(нижние) и контравариантные(верхние) координаты также как и соответствующие им векторы равноправны.

Опускание и поднимание индексов осуществляем с помощью метрических коэффициентов.

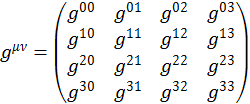
Будем считать, что

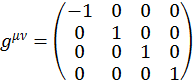(1.2.15)

Если индексы µ и ν опускаются или поднимаются, то при опускании нуля знак коэффициента изменится на противоположный, а при опускании и поднимании индексов 1, 2, 3 ничего не меняется.

Например,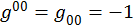

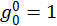
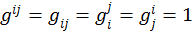
Таким образом, получаем:

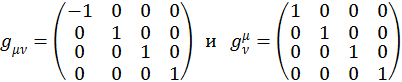(1.2.16)

Если какой-то индекс в формуле встречается два раза на разных высотах, то по нему будет производится суммирование от 0 до 3.

Математически это записывается так:

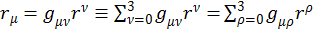(1.2.15)

Согласно правилу Эйнштейна знак суммы по двум одинаковым индексам в дальнейшем будем опускать.

Повторяющиеся индексы будем называть немыми, так как для всех можно использовать любую греческую букву (ρ,λ,…).

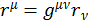(1.2.15)

Проверим это соотношение для конкретных значений индекса µ.

Пусть µ=0:

Пусть теперь μ=1:

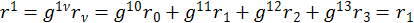, ч. т.д.

§ 1.3. Преобразования Лоренца для координат и времени

Мы пока знаем один четырехмерный вектор . Найдем закон преобразования координат при переходе из одной системы координат к другой. Преобразования Галилея не годятся, т. к. из них вытекает абсолютность времени. Докажем это:

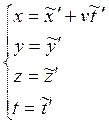(1.3.1)

Будем считать эти преобразования промежуточными (~), и позже они будут заменены на преобразования Лоренца. Подставим это преобразование в выражение для инварианта интервала:

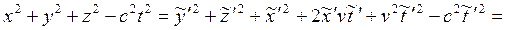
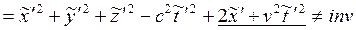(1.3.2)

Таким образом, видно, что инвариантность интервала при таком преобразовании не сохраняется, что противоречит утверждению об инвариантности интервала. Таким образом, у Галилея .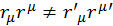

Следовательно, должны существовать другие преобразования. Они были получены Лоренцем. Для вывода мы будем использовать свойства инвариантности интервала. Если считать, что четырехмерный вектор расположен из начала четырехмерных координат, то

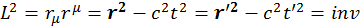(1.3.3)

Преобразуем теперь правую часть выражения (1.3.2) к виду :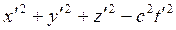

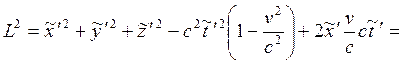
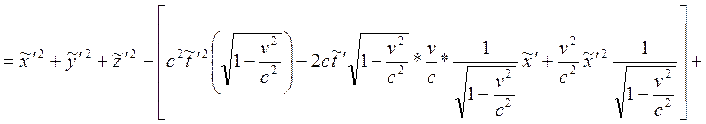
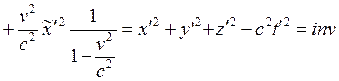
Последнее равенство получится, если произвести замену:

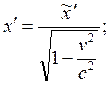
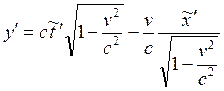(1.3.4)

Если теперь выразить и подставить в преобразование Галилея, получим в итоге преобразования

(1.3.5)

Согласно преобразованиям Галилея :

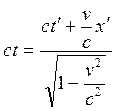. (1.3.6)

Это и есть преобразование Лоренца для времени. Получим теперь преобразование Лоренца для координаты:

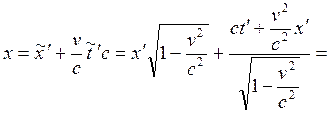
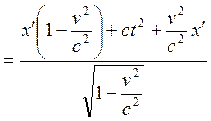(1.3.7)

Окончательно, 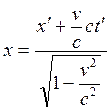. (1.3.8)

В конечном итоге преобразования Лоренца для координат и времени выглядят следующим образом:

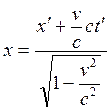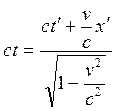; (1.3.9)

Таким образом, мы показали, что будут преобразовываться только время и х-координата, в то время как две другие координаты не преобразуются, т. е. и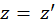

В нерелятивистском приближении преобразования Лоренца переходят в преобразования Галилея, когда v<<c, т. е. <<1.

Иногда нужны обратные преобразования Лоренца (из штрихованной в нештрихованную). Для этого нужно заменить штрихованные величины на нештрихованные и v на –v.

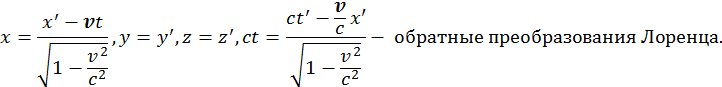
§ 1.4. Преобразования Лоренца для скоростей и углов

После того как были получены преобразования Лоренца для координат и времени, следует определить преобразования Лоренца для скоростей и углов.

Возьмем дифференциалы от преобразований Лоренца для координат и времени:

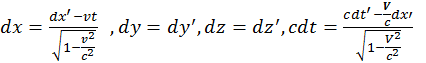(1.4.1)