Происхождение электростатических полей

Полная энергия поля в системе покоя выглядит следующим образом:

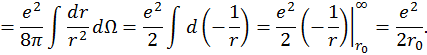
Подставляя выражение для энергии в выражение для собственной массы системы, получим

где – масса “голого” электрона, а – масса электромагнитной “шубы” или электромагнитная масса электрона.

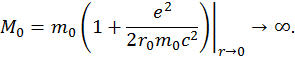
Если (частицы точечные), то собственная масса стремится к бесконечности, а этого не может быть. В связи с этим, принято считать, что классический радиус электрона равен

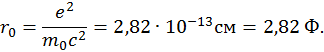
Будем считать, что экспериментально наблюдаемой массой электрона является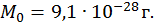

Рассмотрим случай замкнутой системы многих заряженных частиц вместе с полями, которые они создают. Такая система устойчивым образом может существовать только тогда, когда частицы движутся. Не существует устойчивых систем заряженных частиц, находящихся в покое (теорема Ирншоу). Следовательно, будем предполагать, что заряды движутся, но в релятивистском приближении (с небольшими скоростями), поэтому в этом случае магнитное поле отсутствует, т. к. оно ~. При этом полный импульс системы равен нулю.

Тогда собственная масса системы

где энергия частиц равна

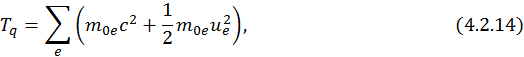
а полная энергия поля

Используя теорему Остроградского-Гаусса, получим

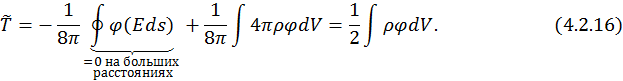
Т. к. плотность заряда

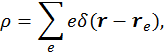
то

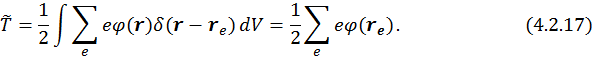
Здесь

а – расстояние от заряда до заряда. Используя данный факт, запишем энергию

Это выражение совпадает с потенциальной энергией системы зарядов (4.1.1):

Тогда собственная масса такой системы примет вид

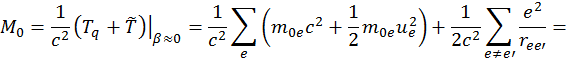
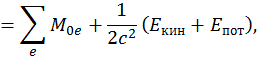
где

Энергия такой системы больше энергии покоя составляющих ее частиц за счет кинетической энергии и потенциальной энергий взаимодействия частиц:

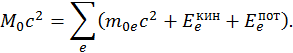
§ 4.3. Происхождение электростатических полей

Кулоновское поле.

В этом параграфе мы ответим на вопрос: как возникают электромагнитные поля. Электромагнитные поля создаются зарядами и токами. Стационарные электрические поля удовлетворяют уравнениям:

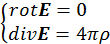, (4.3.1)

где – плотность распределенных в пространстве зарядов.

Если заряды точечные, то

и результирующий заряд системы будет равен

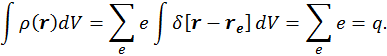
В этих уравнениях напряженность электрического поля связана с потенциалом соотношением:

Но для стационарных полей векторный потенциал не зависит от времени, поэтому

Отсюда получаем уравнение Пуассона

Именно это уравнение по заданному распределению плотности зарядов позволяет найти потенциал, а затем и электрическое поле; дает ответ на вопрос о происхождении электростатического поля.

Рассмотрим пример, когда существует всего один заряд. Поместим его в начало координат. В этом случае

Тогда

Решением уравнения (4.3.5) является потенциал вида

Тогда, используя формулу (4.3.3), можно найти напряженность электрического поля.

Для доказательства (4.3.6) рассмотрим два случая:

а) когда в рассматриваемой нами области пространства точечного заряда. Тогда 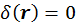,