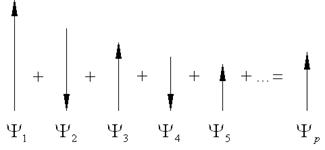
осесимметричные задачи дифракции
Таким образом, волновое поле в точке P записывается в виде
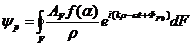 , (6.1)
, (6.1)
где ![]() – амплитуда первичной волны в точке нахождения бесконечно малого элемента
– амплитуда первичной волны в точке нахождения бесконечно малого элемента ![]() волновой поверхности, ρ – расстояние между центром элемента и точкой наблюдения P,
волновой поверхности, ρ – расстояние между центром элемента и точкой наблюдения P, 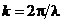 , λ – длина волны первичной волны, ω – частота первичной волны и
, λ – длина волны первичной волны, ω – частота первичной волны и ![]() – начальная фаза вторичной волны, равная фазе первичной волны в точке нахождения рассматриваемого элемента волновой поверхности F, интегрирование ведется по всей волновой поверхности F. Отметим, что явный вид функции
– начальная фаза вторичной волны, равная фазе первичной волны в точке нахождения рассматриваемого элемента волновой поверхности F, интегрирование ведется по всей волновой поверхности F. Отметим, что явный вид функции 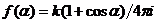 , где
, где 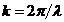 и
и  , был найден Г. Р. Кирхгофом.
, был найден Г. Р. Кирхгофом.
Согласно принципу Гюйгенса-Френеля в формуле (6.1) можно использовать любую замкнутую поверхность, охватывающую источник S первичной волны. Волновая поверхность удобна тем, что во всех ее точках фаза первичной волны имеет одинаковую величину и соответственно одинакова начальная фаза всех вторичных волн. Интеграл в правой части (6.1) определяет модель распространения волны как результат многолучевой интерференции всех вторичных волн, приходящих от всех вспомогательных источников на некоторой замкнутой поверхности в точку наблюдения.
Очевидно, что принцип Гюйгенса-Френеля справедлив только для линейных сред, где выполняется принцип суперпозиции и полное волновое поле в точке наблюдения можно представить в виде суммы вторичных волн.
Принцип Гюйгенса-Френеля выражает самое существенное отличие волнового движения от механического перемещения частицы. В случае механического движения при заданной силе, действующей на частицу, состояние этой частицы в некоторой точке траектории в момент времени t1 однозначно определяет все состояния частицы во все последующие моменты времени t > t1. При волновом движении волновое поле в некоторой точке пространства в момент времени t зависит от распределения волнового поля на всей волновой поверхности, взятой в некоторый момент времени t1<t, т. е. определяется состоянием волнового поля в бесконечно большом числе течек пространства.
Принцип Гюйгенса-Френеля для скалярных волн позволяет приближенно решать некоторые симметричные задачи дифракции света, если не учитывается векторный характер электромагнитных волн, а также особенности их взаимодействия с материалом препятствий. Рассмотрим применение принципа Гюйгенса-Френеля к решению осесимметричных задач дифракции. В этом случае скалярное волновое поле 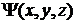 не меняется, то есть инвариантно, при повороте системы координат на произвольный угол вокруг некоторой прямой, являющейся осью симметрии. Если такой осью симметрии является ось z, то волновое поле имеет вид
не меняется, то есть инвариантно, при повороте системы координат на произвольный угол вокруг некоторой прямой, являющейся осью симметрии. Если такой осью симметрии является ось z, то волновое поле имеет вид
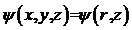 , (6.2)
, (6.2)
где 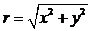 .
.
В качестве примера осесимметричной задачи дифракции рассмотрим падение сферической монохроматической скалярной волны на плоский круглый непрозрачный диск. Центр сферической волны S, точка наблюдения P и центр диска O лежат на одной прямой, перпендикулярной к плоскости диска (рис. 6.4). В данном случае осью симметрии случит прямая SOP.
Рис. 6.4
Для решения такого рода задач дифракции удобно использовать метод зон Френеля, где осуществляется группировка вспомогательных источников вторичных волн в кольцевые зоны в соответствии с осевой симметрией волнового поля. Вторичные волновые поля всех кольцевых зон суммируются в точке наблюдения P с помощью метода векторных диаграмм.
Описание распространения сферической монохроматической волны в свободном пространстве можно рассмотреть как предельный случай решения осесимметричной задачи дифракции, когда радиус диска 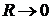 на рис.6.4, и на этом простейшем примере пояснить метод зон Френеля. Ось симметрии есть прямая, проходящая через источник S сферической волны и точку наблюдения P. Выберем волновую поверхность F, радиус которой 0<
на рис.6.4, и на этом простейшем примере пояснить метод зон Френеля. Ось симметрии есть прямая, проходящая через источник S сферической волны и точку наблюдения P. Выберем волновую поверхность F, радиус которой 0< ![]() <OP (рис. 6.5). На этой поверхности волновое поле считается известным, что позволяет с помощью принципа Гюйгенса-Френеля найти волновое поле
<OP (рис. 6.5). На этой поверхности волновое поле считается известным, что позволяет с помощью принципа Гюйгенса-Френеля найти волновое поле ![]() в точке наблюдения P.
в точке наблюдения P.
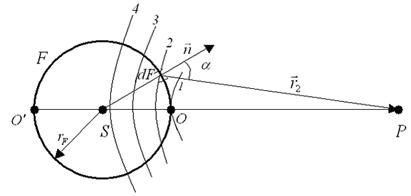
Рис. 6.5
Для разбиения волновой поверхности F на зоны Френеля из точки наблюдения P проведем сферические поверхности, радиусы которых образуют арифметическую прогрессию,
![]()
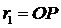 ,
, 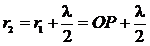 ,
, 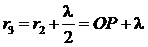 ,…,
,…, 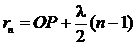 , (6.3)
, (6.3)
где λ – длина волны. Эти сферические поверхности рассекают волновую поверхность F на кольцевые зоны Френеля. Полученные зоны Френеля нумеруются таким образом, чтобы n-я зона Френеля была заключена между сферическими поверхностями с радиусами ![]() и
и ![]() , где n=1,2,3… .
, где n=1,2,3… .
Все вспомогательные источники в пределах каждой зоны Френеля образуют единый источник вторичной волны, которая, вообще говоря, уже не является сферической. Разность фаз вторичных волн, приходящих в точку наблюдения P от соседних зон Френеля, определяется их разностью хода ![]() —
—![]() :
:
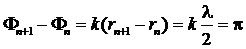 , (6.4)
, (6.4)
т. е. эти волны приходят в точку P в противофазе и при интерференции ослабляют друг друга.
Для достаточно большого расстояния OP площади зон Френеля можно приближенно считать одинаковыми, поэтому с увеличением номера зоны амплитуды вторичных волн монотонно уменьшаются благодаря росту угла α и расстояния r до точки наблюдения. Таким образом, наибольший вклад в волновое поле Ψp дает центральная первая зона Френеля. Вклад последней зоны Френеля, для которой α = π и ƒ(π) = 0, равен нулю (центр последней зоны Френеля находится в точке O’ прямой SP).
Векторную сумму, описывающую вклады вторичных волн в точке наблюдения P, можно изобразить графически следующим образом, где длины векторов определяются амплитудами вторичных волн, а углы между векторами – разностью фаз вторичных волн в точке наблюдения (рис. 6.6).