Тепловое равновесие между излучением и веществом

4. Домашнее задание

4.2 Решение задач

Задача 1. Рассчитайте интерференционную картину совпадений в опыте Брауна-Твисса в случае приема не фотонов, а электронов (см. задачу 1).

Задача 2. При низких температурах в некоторых металлах между электронами возникает эффективное притяжение, и в результате возникают электронные пары (куперовские пары). Эти пары являются бозонами. Почему? Попытайтесь объяснить явление сверхпроводимости для тока, создаваемого куперовскими парами.

занятие 2.1.14

равновесное излучение

2. Тепловое равновесие между излучением и веществом

2.1 Постановка задачи

2.1.1 Распределение энергии между веществом и излучением

При детальном изучении любого природного явления оказывается, что его невозможно объяснить без понимания квантовой природы состояний физических систем. Например, невозможно ответить на вопрос: “Почему никогда не прекращается броуновское движение?”. В том, что этот вопрос не лишен смысла, что в нем заключена глубокая физическая проблема, убеждаемся при детальном рассмотрении теплового равновесия между излучением и веществом.

Молекулы в состоянии теплового равновесия совершают беспорядочное движение, испытывают частые столкновения. Но во время столкновений они движутся с ускорением, и так как состоят из заряженных частиц, то излучают электромагнитные волны. Так что в состоянии теплового равновесия энергия теплового движения должна некоторым образом быть распределенной между излучением и веществом. Вот здесь-то, при подробном рассмотрении равновесия, мы сталкиваемся с парадоксом.

Для проведения детального анализа состояния равновесия возьмем упрощенную модель. Пусть газ из молекул находится внутри кубического сосуда с идеально зеркальными стенками. При столкновении молекул со стенками и между собой они излучают электромагнитные волны. Так как стенки зеркальные, излучение никуда не уходит. Распределение излучения представляет собой систему стоячих волн. Каждая стоячая волна — это колебательная мода, которая ведет себя точно так же, как одномерный гармонический осциллятор со своей собственной частотой. Колебательная система имеет столько мод, сколько у нее степеней свободы. Так как длины волн могут быть как угодно малыми, и мод может быть бесконечно много, электромагнитное излучение имеет бесконечное число степеней свободы.

В курсе молекулярной физики 10 класса утверждалось, что физическая система самопроизвольно переходит из менее вероятных в более вероятные состояния. Установление теплового равновесия — это движение в сторону увеличения энтропии, увеличения беспорядка. Наиболее беспорядочное состояние представляет собой равномерное распределение энергии

системы по степеням свободы. Но, поскольку число степеней свободы излучения бесконечно, из условия максимума беспорядка, вся тепловая энергия должна поровну распределиться между модами излучения. А так как на каждую моду в состоянии теплового равновесия должна приходиться средняя энергия kБT (по kБT/2 на кинетическую и потенциальную энергии), то при распределении конечной энергии по бесконечному числу степеней свободы мы должны получить нулевую температуру. Больше того, практически вся энергия должна приходиться на коротковолновое излучение с бесконечно малой длиной волны. Из данного рассмотрения следует, что никакого теплового движения ни молекулы, ни броуновские частицы не должны совершать. В мире должна царить мертвая недвижность! Одна из задач данного занятия состоит в том, чтобы показать, как квантовая механика объясняет несоответствие нарисованной картины реальной природе.

2.1.2 Проблема спектрального распределения равновесного
излучения

Если рассматривать тепловое излучение через спектроскоп, то видно радужное распределение света. Участки радуги имеют разные яркости. Есть наиболее яркие (максимум спектральной плотности) и есть менее яркие. При повышении температуры максимум спектральной плотности смещается в область коротких волн. Экспериментально наблюдаемое распределение плотности излучения по спектру (спектральная плотность — это интенсивность излучения, переносимая волнами, частоты которых заключены в интервале от w до w+dw, отнесенная к dw) многие физики безуспешно пытались объяснить в начале нашего века. Была назначена международная премия за решение этой задачи. Решение удалось получить М. Планку в 1900 г. С этого началась история квантовой механики. В данном занятии будут рассмотрены основные идеи теории Планка.

2.2 Средняя энергия электромагнитной моды в тепловом
равновесии

Рассмотрим описанную выше упрощенную модель физической системы, находящейся в тепловом равновесии. Пусть газ из молекул находится внутри кубического сосуда с длиной ребра, равной L с идеально зеркальными стенками. Пусть также, абсолютная температура газа равна T. Определим, какая энергия в среднем должна приходиться на электромагнитную моду с частотой w.

Поскольку стоячая волна является одномерным гармоническим осциллятором, ее энергетический спектр описывается формулой:
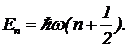(1)
Энергия основного состояния моды не участвует в теплообмене, поэтому будем отсчитывать энергию от основного состояния, то есть
En=ћwn. (2)
Чтобы вычислить среднее значение энергии волны данной частоты разобьем множество всех волн этой частоты в сосуде на группы. Первая группа из N1 волн — это волны в первом возбужденном состоянии, то есть находящиеся на уровне с энергией E1=ћw. Вторая группа из N2 волн — это волны во втором возбужденном состоянии, то есть находящиеся на уровне с энергией E2=2ћw. Третья группа из N3 волн — это волны в третьем возбужденном состоянии, т. е. находящиеся на уровне с энергией E3=3ћw. И так далее. Среднюю энергию можно найти так: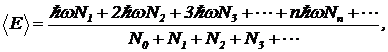
(3)
где N0 — число волн в основном состоянии. Заметим, что
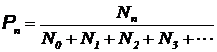(4)
равна доле волн, находящихся в n-ом возбужденном состоянии, или вероятности того, что наугад выбранная волна с частотой w находится на n-ом уровне. Таким образом, формула (3) может быть записана так:
(5)

Вероятности нахождения в возбужденных состояниях, согласно выводам теории равновесных состояний (см. материал 10 класса, тема 1.3):

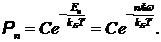(6)

Постоянную С можно определить из условия, что мода наверняка находится на каком-нибудь уровне, то есть

P1+P2+P3+…+Pn+…=1. (7)

Так что имеем
(8)

В левой части уравнения (8) стоит геометрическая прогрессия S=1+q+q2+ q3+…+qn+ с основанием 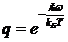. Вспомним, что сумма бесконечной геометрической прогрессии равна 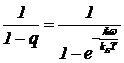, поэтому

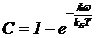(9)

и выражение средней энергии принимает вид: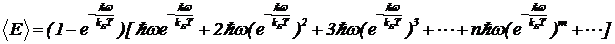
Можно заметить, что сумма в квадратной скобке без множителя ћw представляет собой минус производную от суммы в уравнении (8) по переменной —

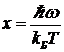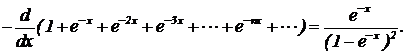
Итак, выражение средней энергии, приходящейся на одну электромагнитную моду частоты w, принимает вид:

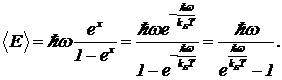(10)

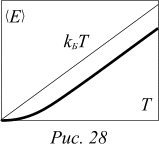
Это знаменитая формула Планка для средней энергии гармонического осциллятора, находящегося в состоянии теплового равновесия с окружающей средой. В нашем случае осциллятор — это электромагнитная мода, а окружающая среда — молекулы газа. На рисунке 28 приведен график зависимости средней энергии одной из мод от абсолютной температуры.

Проанализируем это выражение. При 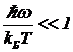справедлива приближенная оценка
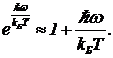(11)
Тогда
áEñ»kБT, (12)
что согласуется с классической формулой. Так что можно сделать вывод, что классическая теория теплового равновесия справедлива для высоких температур и разностей уровней, гораздо меньших, чем kБT.