Уравнение 1-го закона термодинамики
1. Первый закон термодинамики устанавливает, что внутренняя энергия ТС является однозначной функцией ее состояния, которая не изменяется при отсутствии внешних воздействий при любых процессах внутри термодинамической системы (равновесных и неравновесных).
2. Работа может совершаться за счет изменения внутренней энергии и за счет сообщения системе теплоты.
3. В круговом процессе изменение внутренней энергии не происходит, и работа совершается только за счет получения системой теплоты от внешних источников.
4. Появление работы всегда сопровождается затратами других видов энергии, т. е. вечный двигатель 1-го рода неосуществим. Вечный двигатель 1-го рода – это периодически действующая машина, которая совершает работу, не заимствуя энергию извне.
5.2. Уравнение 1-го закона термодинамики для проточной термодинамической системы
Проточная система является частным случаем открытой ТС, когда вещество на одном участке границы ТС входит в систему, а на другом участке – выходит из ТС. В этом случае рассматривается схема течения вещества относительно неподвижных осей координат, связанных с границей ТС, как представлено на прилагаемом рисунке.
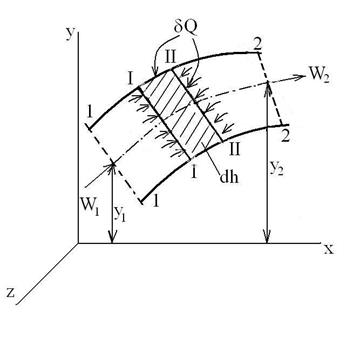
На элемент dh в сечении I-I площадью F действует давление – р при скорости течения потока рабочего тела – W, а в сечении II-II площадью (F+dF) – давление (р+dp) при скорости (W+dW), и подводится теплота ![]() .
.
Тогда в уравнение 1-го закона термодинамики дополнительно к внутренней энергии необходимо учитывать, что в проточной ТС поток рабочего тела несет с собой кинетическую энергию своего движения относительно границ ТС, равную d(mW2/2), а потенциальная энергия потока рабочего тела в поле внешних сил (в поле тяготения Земли) может изменяться gd(my), где у – пьезометрическая высота, g – ускорение силы тяжести. Эти виды энергии входят в уравнение 1-го закона термодинамики в качестве самостоятельных членов.
Кроме того, над рабочим телом, поступающим в ТС, совершается работа проталкивания (вытеснения) ℒпрот=d(pV) по преодолению внутреннего давления ТС внешней силой и давления окружающей среды при выводе рабочего тела из ТС. При этом полагается, что процессы ввода-вывода рабочего тела являются равновесными.
Работа проталкивания d(pV) – функция состояния и определяется только начальными и конечными значениями параметров, а ее дифференциал является полным дифференциалом:
ℒпрот=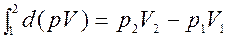 ,
, 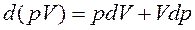 ,
,
где pdV – работа расширения; Vdp – располагаемая работа (работа перемещения), которая идет на изменение кинетической энергии рабочего тела и преодоление сил трения.
Термодинамическое рабочее тело может также производить техническую работу ![]() ℒтехн при перемещении канала с рабочим телом в пространстве, например, при вращении ротора турбины.
ℒтехн при перемещении канала с рабочим телом в пространстве, например, при вращении ротора турбины.
Таким образом, уравнение 1-го закона термодинамики для проточной ТС при m=const будет иметь вид:
 ℒтехн, Дж/с.
ℒтехн, Дж/с.
Для однородного рабочего тела при m=1кг/с
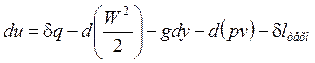 , Дж/кг.
, Дж/кг.
При 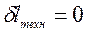 и
и 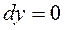
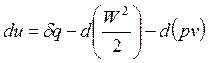 , Дж/кг.
, Дж/кг.
Так как 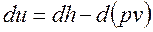 , то уравнение 1-го закона термодинамики, выраженное через энтальпию, будет иметь вид:
, то уравнение 1-го закона термодинамики, выраженное через энтальпию, будет иметь вид:
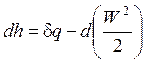 , Дж/кг.
, Дж/кг.
Эти уравнения пригодны для исследования термодинамических процессов во всех типах тепловых двигателей, где имеется движение рабочего тела по тракту двигателя (реактивные двигатели, газотурбинные установки и др.).
Относительно осей координат, которые движутся вместе с центром масс рассматриваемого элемента потока, энергетические превращения можно описать уравнением Бернулли:
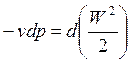 .
.
Тогда уравнения 1-го закона термодинамики для подвижных осей координат при 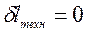 и
и 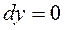 будут иметь вид:
будут иметь вид:
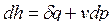 ,
,
и 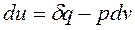 , которые аналогичны по форме записи уравнениям первого закона термодинамики для неподвижной закрытой термодинамической системы.
, которые аналогичны по форме записи уравнениям первого закона термодинамики для неподвижной закрытой термодинамической системы.
Запишем уравнение 1-го закона термодинамики для конечного процесса в проточной ТС в виде:
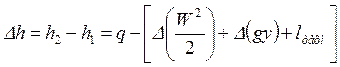 ,
,
где 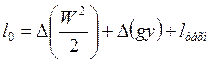 — сумма величин механической природы, называемой располагаемой работой. В тепловых машинах
— сумма величин механической природы, называемой располагаемой работой. В тепловых машинах 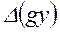 =0.
=0.
Тогда в турбинах 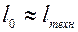 , а в соплах
, а в соплах 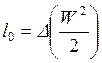 . Техническая работа
. Техническая работа ![]() в турбине может совершаться за счет уменьшения кинетической энергии потока рабочего тела или за счет уменьшения его потенциальной энергии при падении потока воды с верхнего уровня на нижний уровень.
в турбине может совершаться за счет уменьшения кинетической энергии потока рабочего тела или за счет уменьшения его потенциальной энергии при падении потока воды с верхнего уровня на нижний уровень.
Приведенные в данном разделе уравнения выводились при использовании параметров состояния в сечениях на входе и выходе из системы, где состояния рабочего тела полагались равновесными. Поэтому эти уравнения справедливы и в случае протекания неравновесных процессов внутри термодинамической системы, например, если в ТС происходят химические реакции, потери на трение и др.
ГЛАВА 6. ВТОРОЙ ЗАКОН ТЕРМОДИНАМИКИ
6.1. Сущность второго закона термодинамики. Равновесные и неравновесные состояния, обратимые и необратимые процессы
Второй закон термодинамики устанавливает существование у всякой равновесной термодинамической системы однозначной функции состояния – энтропии S.
Понятие энтропии вводится в феноменологической термодинамике с помощью выражения dS=![]() , в соответствии с которым при подводе к ТС порции теплоты
, в соответствии с которым при подводе к ТС порции теплоты ![]() энтропия системы возрастает. Температура Т в этом выражении есть температура на границе ТС в точке, где подводится порция теплоты
энтропия системы возрастает. Температура Т в этом выражении есть температура на границе ТС в точке, где подводится порция теплоты ![]() . С помощью этой специальной функции состояния можно математически описать 2-ой закон термодинамики.
. С помощью этой специальной функции состояния можно математически описать 2-ой закон термодинамики.
ТС находится в состоянии равновесия, если после ее изоляции от окружающей среды в ней не наблюдается никаких изменений, и в неравновесном состоянии, если после ее изоляции в ней обнаруживаются какие-либо изменения. Эти изменения в изолированной системе протекают самопроизвольно, и со временем система приходит в равновесное состояние. Процесс является неравновесным, если при его совершении ТС хотя бы в одной точке процесса находится в неравновесном состоянии. Неравновесные состояния ТС могут быть связаны либо с локальной неравновесностью в точке, либо с объемной неравновесностью из-за различия температур, давлений и других параметров в различных элементах объема ТС. При объемной неравновесности ТС для проведения термодинамических расчетов объем ТС можно разбить на малые объемы, в пределах которых перепады параметров (р, Т и др.) малы и состояния в пределах каждого из объемов можно считать локально равновесным.


