Квантовое движение частиц

Лекция № 13

Квантовое движение частиц

1. Свободное движение частиц.

2. Стационарные состояния частицы в потенциальной яме.

3. Квантование энергетического спектра гармонического осциллятора.

4. Стационарные состояния атома водорода.

5. Переходы между стационарными состояниями. Правила отбора.

6. Туннельный эффект и надбарьерное отражение.

В нерелятивистской квантовой механике состояние частицы описывается посредством волновой функции , удовлетворяющей уравнению Шредингера

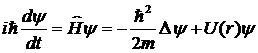, (13.1)

где m – масса частицы, ћ = h/2π, h – постоянная Планка,

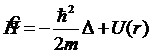(13.2)

— оператор полной энергии частицы в потенциальном поле U(r) и

.

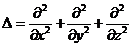Все наблюдаемые физические характеристики частицы определяются с помощью волновой функции 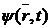, которую часто называют комплексной амплитудой вероятности.

Для получения единственного решения уравнения в частных производных (13.1) необходимо задать начальное состояние частицы в некоторый момент времени t=0

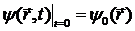(13.3)

и определенные граничные условия на поверхности, ограничивающей область возможного движения частицы. В частности, граничные условия могут задаваться на бесконечности, где r → ∞.

Особый интерес представляют стационарные состояния частицы, где ее энергия Е является точно определенной, а все усреднённые с помощью волновой функции динамические характеристики системы не зависят от времени. Стационарные состояния возможны только для замкнутой системы и описываются волновой функцией строго определенного вида

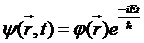, (13.4)

где координатная часть волновой функции есть решение стационарного уравнения Шредингера

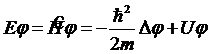, (13.5)

получаемого путем подстановки функции (13.4) в уравнение (13.1). Стационарное уравнение Шредингера (13.5) определяет собственные функции и собственные значения оператора полной энергии Ĥ (оператора Гамильтона), который для замкнутой системы не содержит времени.

Свойства стационарных состояний частицы зависят от ее потенциальной энергии U(r), а также размерности, формы и размеров той пространственной области, в которой происходит движение частицы.

Рассмотрим свободное (U=0) движение частицы в неограниченном трехмерном пространстве, когда стационарное уравнение Шредингера (13.5) принимает вид

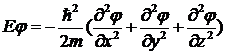. (13.6)

Одно из решений уравнения (13.6) записывается следующим образом:

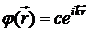, (13.7)

где с – комплексная постоянная, определяемая условием нормировки φ, а вектор удовлетворяет соотношению

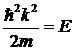. (13.8)

Если ввести импульс частицы

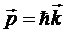, (13.9)

то полная волновая функция (13.4) для стационарного состояния частицы в свободном пространстве

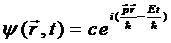(13.10)

есть волна де Бройля, бегущая в направлении вектора . Длина волны де Бройля определяется известной формулой

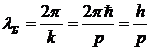. (13.11)

Выражения (13.8)-(13.11) описывают нерелятивистское движение свободной частицы.

Стационарное состояние свободной частицы характеризуется не только точно определенным значением ее кинетической энергии Е, но и точно определенным импульсом . Это возможно благодаря тому, что операторы кинетической энергии и импульса частицы коммутируют. Отметим также, что значения кинетической энергии и импульса связаны между собой классической формулой (13.8).

С другой стороны операторы координат не коммутируют с операторами соответствующих компонент импульса, поэтому в соответствии с принципом неопределенностей Гейзенберга пространственное положение частицы полностью неопределенно. Плотность вероятности обнаружения частицы в любом элементе пространства согласно формуле

dP=|ψ|2dV=|c|2dV (13.12)

есть величина постоянная и равна

dP/dV=|c|2. (13.13)

В этом случае говорят, что частица равномерно «размазана» по всему пространству. Законы квантовой механики не позволяют локализовать свободную частицу с заданным импульсом в какой-либо заданной точке пространства.

Пространственную локализацию частицы в конечной области пространства можно осуществить с помощью потенциальной энергии взаимодействия. Допустим, что частица массой m совершает одномерное движение вдоль оси х, находясь в бесконечно глубокой потенциальной яме прямоугольной формы шириной d. Зависимость потенциальной энергии U от координаты х приведена на рис.13.1. На границах ямы x=0 и x=d потенциальная энергия скачком возрастает от 0 до ∞.

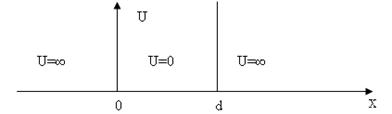
Рис. 13.1.

Для области 0<х<d внутри потенциальной ямы стационарное уравнение Шредингера (13.6) запишется в следующем виде:

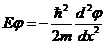. (13.14)

За пределами потенциальной ямы частица находиться не может, поскольку это требует бесконечной энергии. В связи с этим

φ≡0, х <0 или х >d. (13.15)

В силу непрерывности волновой функции на границах потенциальной ямы должно выполняться граничное условие

φ|x=0 = φ|x=d =0 . (13.16)

Решение граничной задачи (13.14)-(13.16) имеет вид:

φ=с sinknx 0≤x≤d, (13.17)

где

knd=πn , n=1,2,3, … . (13.18)

Соотношение (13.18) определяет дискретный энергетический спектр частицы стационарных состояний в рассматриваемой потенциальной яме. Подставляя функцию φ (13.17) в уравнение (13.14), с учетом (13.18) получим:

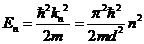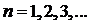, . (13.19)

Принципиальным является то обстоятельство, что наименьшая кинетическая энергия частицы в основном состоянии с n=1 отлична от нуля:

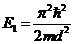. (13.20)

Таким образом, согласно квантовым законам в ограниченной области существует самодвижение частицы без каких-либо внешних воздействий, некая внутренняя активность частиц, что является в некотором смысле аналогом движения по инерции в классической механике. С другой стороны, формула (13.20) показывает, что для локализации частицы требуется определенная энергия, причем величина этой энергии растет с уменьшением линейного размера локализации d как 1/d2.

В заключение отметим, что постоянная c волновой функции (13.17) находится из условия нормировки