Метод суперпозиции (наложения)

4.5. Вычисляют контурные ЭДС как алгебраические суммы ЭДС, входящих в данный контур, и обозначают , при этом ЭДС, условные положительные направления которых совпадают с принятым направлением контурного тока, записывают со знаком “+”, в противоположном случае – со знаком “–”.

4.6.Записывают систему линейных уравнений для контурных токов в следующей канонической форме: коэффициенты главной диагонали левой части системы записывают со знаком “+”, все остальные коэффициенты 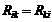со знаком “–”; в правой части уравнения записываются соответствующие контурные ЭДС :

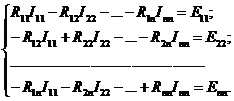
11

4.7. Решают полученную систему линейных уравнений размерности относительно контурных токов , при этом, если в результате решения какой-либо контурный ток получается со знаком “–”, его первоначально принятое условное положительное направление необходимо изменить на противоположное.

4.8. Определяют величины и направления токов в ветвях: если ветвь принадлежит одному контуру, то ток в ней равен контурному; если ветвь общая для двух смежных контуров, то ток в ней равен алгебраической сумме токов и . Направление тока в ветви, общей для двух смежных контуров, определяется направлением большего по модулю контурного тока.

5 МЕТОД СУПЕРПОЗИЦИИ (НАЛОЖЕНИЯ)

Этот метод основан на следующем физическом принципе, свойственном линейным цепям: воздействие нескольких источников ЭДС на каждый элемент линейной цепи можно рассматривать как результат воздействия на данный элемент каждого источника в отдельности, независимо от всех других.

Данный метод требует большой точности и большого объема вычислений, однако он наиболее нагляден, так как позволяет определить влияние каждого источника в отдельности на процессы в электрических цепях.

При использовании метода суперпозиции можно рекомендовать такую последовательность расчета.

5.1.Из рассчитываемой схемы удаляют все источники электроэнергии, кроме одного. При этом для удаленных источников оставляют в схеме их внутренние сопротивления.

5.2.Составляют новую схему с одним источником, упрощают ее с помощью методов преобразования, указанных в разделе 2.2 настоящих методических указаний, и определяют для нее токи в ветвях , т. е. рассчитывают образовавшуюся простую схему методом «свертывания».

Примечание: Ветви при окончательном определении токов должны соответствовать первоначальной схеме. Направления токов в ветвях определяются полярностью оставленного источника.

5.1.Подобным образом рассчитывают поочередно токи , , и т. п., создаваемые всеми другими источниками.

5.2.Рассчитывают результирующий ток в каждой ветви как алгебраическую сумму частных токов , , и т. д.

12

6 МЕТОД УЗЛОВОГО НАПРЯЖЕНИЯ

Этот метод позволяет весьма просто произвести анализ и расчет цепи, содержащей несколько параллельно соединенных активных и пассивных ветвей.

При использовании данного метода можно рекомендовать такую последовательность расчета.

6.1.Выбирают условное положительное направление напряжения действующего между двумя узлами (полюсами) схемы, относительно которых все ветви включены параллельно.

6.2.Выбирают и обозначают на схеме условные положительные направления токов в ветвях: в активных – по направлению ЭДС, в пассивных – по напряжению

6.3.Определяют величину узлового напряжения

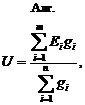
где – проводимость -й ветви (с учетом внутренних сопротивлений источников); – ЭДС, действующая в -й ветви; – общее количество ветвей; – количество активных ветвей.

Примечание: Слагаемое в числителе записывается со знаком “–”, если ЭДС направлена согласно с и со знаком “+”, если встречно с Если в результате решения напряжение получается со знаком “–”, то это напряжение противоположно первоначально принятому.

6.4.Определяют токи в ветвях в соответствии со II законом Кирхгофа для каждой ветви:

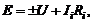
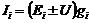
6.5.Если в результате решения какой-либо ток получает знак “–”, это означает, что его условное положительное направление противоположно ранее принятому.

7 МЕТОД ЭКВИВАЛЕНТНОГО ГЕНЕРАТОРА

Данный метод дает возможность упростить анализ и расчет

13

электрических цепей в том случае, когда требуется определить ток лишь в

одной из ветвей или упростить схему, заменив часть ее активным двухполюсником и эквивалентным генератором со своими ЭДС и внутренним сопротивлением , как показано на примере рис. 7.1, 7.2.