Потенциал электрического поля

6.  Дана нить, равномерно заряженная по длине с линейной плотностью заряда . Параллельно нити на расстоянии расположен квадрат. Сторона квадрата . Вычислите поток вектора напряженности электрического поля через поверхность данного квадрата.

7.  Дана бесконечная цилиндрическая поверхность с радиусом основания и равномерно заряженная по поверхности с плотностью заряда . На расстоянии от оси находится точка . Вычислите напряженность электрического поля в данной точке.

Дополнительный блок задач

8.  Тонкое круглое кольцо радиуса состоит из двух равномерно и противоположно заряженных полуколец с линейными плотностями заряда и . Найдите напряженность электрического поля на оси кольца.

9.  Нить расположена по дуге окружности радиусом и видна из ее центра под углом . Нить заряжена с линейной плотностью заряда . Найдите напряженность электрического поля в центре окружности. Рассмотрите предельный случай – нить расположена по окружности радиуса .

10.Найдите напряженность электрического поля в центре шара радиуса , объемная плотность которого равна 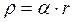, где – расстояние от центра шара до точки наблюдения.

11.Две длинные параллельные нити равномерно заряжены с линейной плотностью заряда 0,5 мк Кл/м каждая. Расстояние между нитями равно 0,45 м. Найдите максимальное значение напряженности электрического поля в плоскости симметрии этой системы.

12.Полубесконечный цилиндр радиуса заряжен равномерно по поверхности так, что на единицу его длины приходится заряд . Найдите напряженность электрического поля в центре основания цилиндра.

Практическое занятие №2

Потенциал электрического поля

Краткие теоретические сведения

Решением уравнения 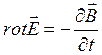в статическом случае (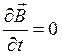) является функция, удовлетворяющая условию 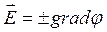. Исторически было выбрано решени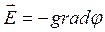е , где – потенциал точки пространства, в которой напряженность электрического поля равна .

Учитывая связь напряженности и потенциала электрического поля, потенциал – это работа сил электрического поля по переносу единичного положительного заряда из точки наблюдения на бесконечно большое расстояние, или

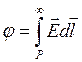. (2.1)

Разность потенциалов двух точек поля можно рассчитать как отношение работы сил электрического поля к величине переносимого заряда , то есть

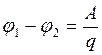. (2.2)

Потенциал электрического поля – скалярная величина, и в случае наличия нескольких зарядов его рассчитывают в соответствии с принципом суперпозиции

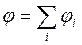. (2.3)

Если заряд распределен непрерывно по линии, поверхности или объему, суммирование заменяем интегрированием. Например, для потенциала заряда, распределенного по объему, получим

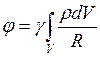. (2.4)

Систему из двух одинаковых по модулю разноименных зарядов и называют диполем и характеризуют дипольным моментом . Потенциал электрического поля диполя на большом расстоянии от него описывается формулой

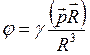. (2.5)

В некоторых случаях (если известно выражение для напряженности электрического поля) для нахождения потенциала можно воспользоваться условием .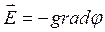

Темы для развернутых ответов

1.  Потенциал электрического поля.

2.  Потенциал электрического поля диполя и его расчет.

Литература: [1], глава 2, §14;[3], глава 1, §8, 10.

Основной блок задач

1.  Дана бесконечная нить, заряженная с поверхностной плотностью заряда . Точка наблюдения находится на расстоянии от нити. Рассчитайте потенциал электрического поля в данной точке.

2.  Дана бесконечная плоскость, равномерно заряженная по поверхности с плотностью заряда . Найдите потенциал электрического поля в точке наблюдения , не принадлежащей плоскости.