Сдвиг и кручение

Таким образом,

.

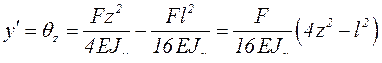Подставляя значение z = 0, найдём угол поворота сечения балки в опоре А:

.

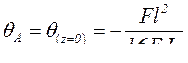Интегрируя полученное выражение для , определим прогибы балки :

.

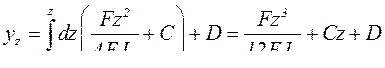Постоянную интегрирования D найдём из условия равенства нулю прогиба балки в опоре А при :

.

Аналитическое выражение для прогиба балки примет вид:

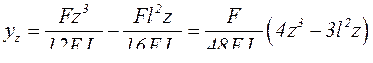
Максимальный прогиб балки будет в точке С при :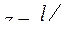

.

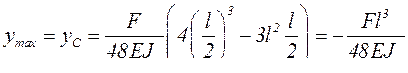Отрицательное значение перемещение точки С означает, что оно не совпадает с направлением оси у.

Вопросы для самопроверки

1.В чём отличие между изгибом прямым и косым, чистым и поперечным?

2. Какие внутренние силы возникают в поперечных сечениях балки при изгибе?

3. Какие правила знаков приняты при изгибе для поперечных сил и изгибающих моментов?

4. Как определяется поперечная сила и изгибающий момент в сечениях балки при изгибе?

5. Какие типы опор применяются для закрепления балок к основанию?

6. Какие уравнения используются для определения значений опорных реакций?

7. Какая дифференциальная зависимость существует между изгибающим моментом, поперечной силой и интенсивностью распределённой нагрузки, перпендикулярной к оси балки?

8. Чему равна поперечная сила в сечениях балки, в которых изгибающий момент достигает экстремальных значений?

9. По каким законам изменяется поперечная сила и изгибающий момент по длине балки при отсутствии распределённой нагрузки?

10. Как изменяется поперечная сила в сечении, в котором приложена сосредоточенная сила, перпендикулярная к оси балки?

11. Как изменяется изгибающий момент в сечении, в котором к балке приложен сосредоточенный внешний момент?

12. В чём заключается проверка эпюр и ?

13. Какой вид имеет эпюры для балки, заделанной одним концом:

а) от сосредоточенной силы, перпендикулярной оси балки, приложенной на её свободном конце;

б) от сосредоточенного момента, приложенного на свободном конце балки;

в) от равномерно распределённой нагрузки, перпендикулярной оси балки, действующей по всей еёе длине?

14. Как распределены нормальные напряжения в поперечных сечениях балки при изгибе?

5. Сдвиг и кручение

При сдвиге и кручении на боковых гранях выделенного элемента действуют только касательные напряжения. В том и в другом случае частицы элемента конструкции стремятся сдвинуться относительно друг друга в плоскости сечения, т. е. имеет место деформация сдвига.

5.1. Сдвиг

Сдвигом называется такой вид деформации стержня, при котором в поперечном сечении возникает только поперечная (перерезывающая) сила. Они вызывают касательные напряжения, или напряжения сдвига.

Явление сдвига можно наблюдать при перерезывании полосы ножницами (рис. 23). Из рисунка видно, что сдвиг одной части относительно другой возникает в том случае, когда плечо h мало. При большом плече h сдвиг сопровождается изгибом. При увеличении сил деформация завершается перерезыванием полосы.

Закрепим полосу по плоскости 1–4 (рис. 23а). Рассмотрим сдвигаемый элемент полосы в виде, показанном на рис 23б.

Действие отброшенной правой части на левую представим сдвигающими силами, равнодействующая которых приводится к поперечной силе , равной по модулю внешней силе .

В сечении возникают касательные напряжения . Суммируя их по всей площади сечения, получим поперечную силу

. (5.1)

Распределение касательных напряжений по сечению неравномерное, однако, для небольших толщин его можно считать равномерным, т. е. постоянным, и тогда

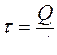. (5.2)

По формуле (5.2) определяют касательные напряжения. В заделке возникают и нормальные напряжения от изгиба, которыми часто пренебрегают ввиду их малости.

При воздействии силы плоскость 2−2′−3′−3 (рис. 23б) перемещается вертикально относительно заделки на величину (рис. 23в), Пренебрегая малыми величинами, можно считать, что при сдвиге объём не изменяется, а происходит лишь изменение формы: прямоугольник 1−2−3−4 превращается в параллелограмм 1−2′−3′−4. Угол сдвига определяет изменение формы – искажение углов первоначального параллелепипеда.

Аналогично закону Гука при растяжении в пределах упругости, касательное напряжение при сдвиге прямо пропорционально относительному сдвигу :

. (5.4)

Формула (5.4) выражает закон Гука при сдвиге. Параметр называется модулем упругости при сдвиге (модуль сдвига).

Существует зависимость между модулем упругости при сдвиге и модулем продольной упругости при растяжении :

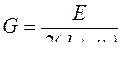. (5.5)

Подставив значения и (формулы (5.2) и (5.3)) в (5.4), получим формулу для определения значения абсолютного сдвига:

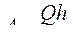. (5.6)

Условие прочности при сдвиге имеет вид:

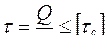, (5.7)