Теорема о переносе пары сил в параллельную плоскость

а)

б)

в)

Рис. 22. Теорема об эквивалентности пар сил

8.3. ТЕОРЕМА О ПЕРЕНОСЕ ПАРЫ СИЛ В ПАРАЛЛЕЛЬНУЮ ПЛОСКОСТЬ

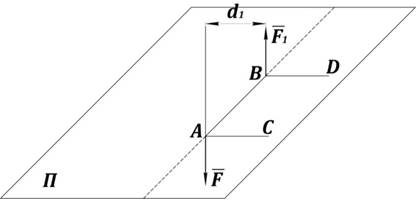
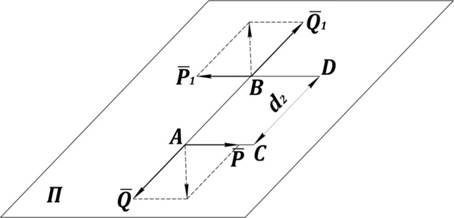
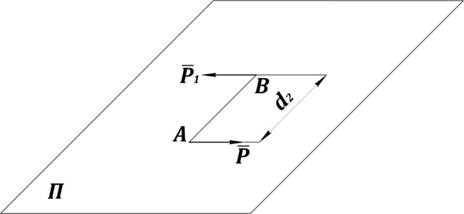
Формулировка: пару сил можно переносить в плоскость, параллельную данной, не меняя её действия (рис. 23).

Доказательство:

В плоскости I была пара сил и .

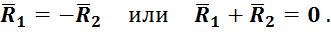
Силы, внесённые в плоскость II:

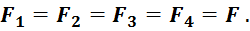
В точку перенесены силы и , и , выполнена их замена на уравновешенные силы и , т. е. эти силы исключены.

Таким образом, в плоскости II осталась пара сил и , эквивалентная паре сил и , бывшей в плоскости I.

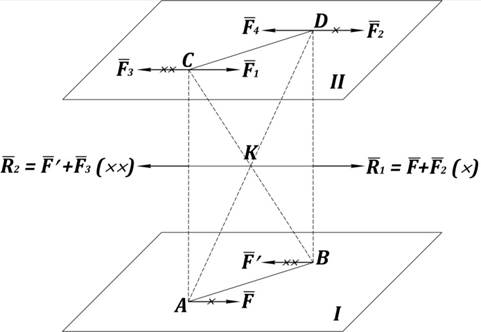
Рис. 23. Теорема о переносе пары сил в параллельную плоскость

Из выше доказанного (см. предыдущие теоремы) следуют три свойства пары сил:

1) пару сил можно переносить куда угодно в плоскости пары, при этом её действие не меняется;

2) можно произвольно менять модули сил и плечи, сохраняя неизменным момент пары сил;

3) пару сил можно переносить в плоскость параллельную данной, при этом её действие не изменится.

Поэтому вектор пары сил в связи с возможным переносом называется свободным.

8.4. ТЕОРЕМА О СЛОЖЕНИИ ПАР СИЛ В ПРОСТРАНСТВЕ

Формулировка: система пар сил в пространстве эквивалентна одной паре с моментом, равным геометрической сумме моментов слагаемых пар (рис. 24).

Доказательство:

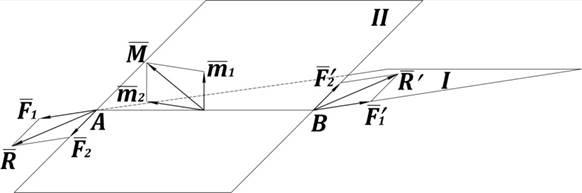
Рис. 24. Теорема о сложении пар сил в пространстве

В плоскости I: и , .

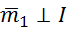В плоскости II: и , .

Выполнена замена:

Пара сил и эквивалентна двум исходным парам.

Так как 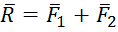, то можно записать

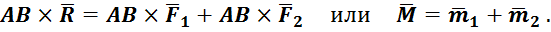
В общем случае

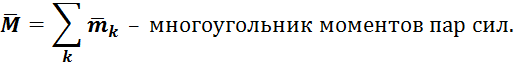
9. ТЕОРЕМА О ПАРАЛЛЕЛЬНОМ ПЕРЕНОСЕ СИЛЫ

(ПРИВЕДЕНИЕ СИЛЫК ЗАДАННОМУ ЦЕНТРУ)

Формулировка: силу, приложенную к телу, можно переносить параллельно из данной точки в другую, прибавляя пару сил с моментом, равным моменту переносимой силы до другой точки (рис. 25).

Доказательство:

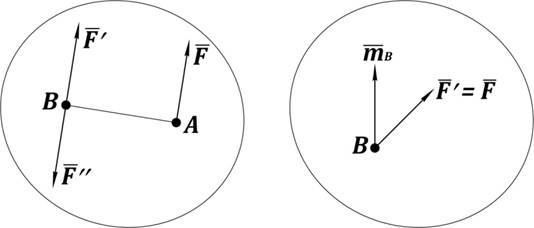
Рис. 25. Теорема о параллельном переносе силы

и – дополнительные силы:

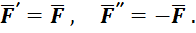
Пара сил и образуют момент .

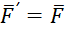В точке остаётся сила и появляется момент .

10. ПРИВЕДЕНИЕ ПРОИЗВОЛЬНОЙ

( ПЛОСКОЙ ИЛИ ПРОСТРАНСТВЕННОЙ)

СИСТЕМЫ СИЛ К ДАННОМУ ЦЕНТРУ

В этом случае система сил , , , … , заменяется одной силой 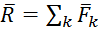и суммой моментов, а именно произведений каждой из этих сил на расстояние от точки её приложения до некоторого центра